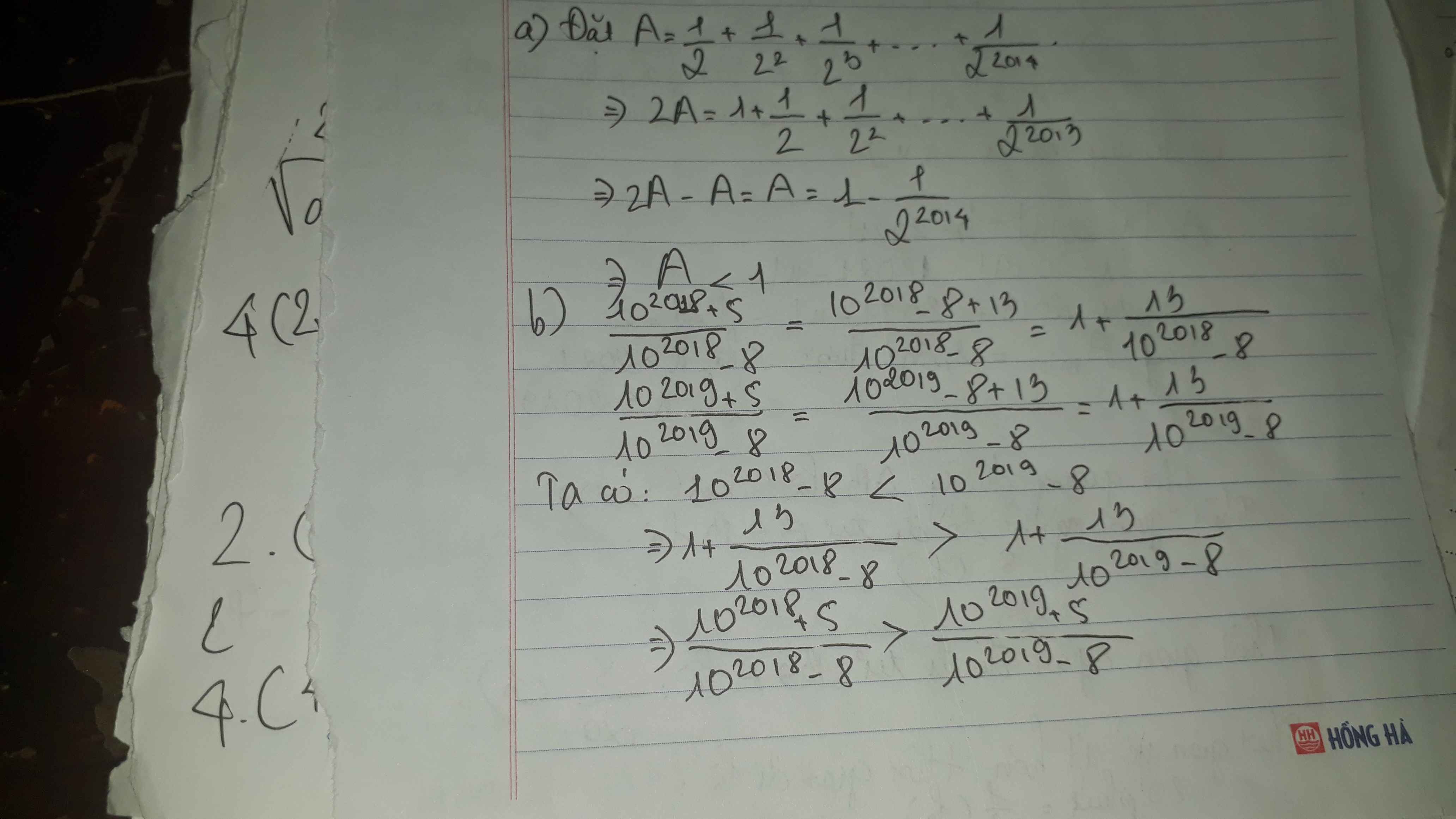\(A>\dfrac{2^{2018}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{3^{2019}}{2^{2018}+3^{2019}+5^{2020}}+\dfrac{5^{2020}}{5^{2020}+2^{2018}+3^{2019}}=1\)

\(B< \dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{2019\cdot2020}\)

\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2019}-\dfrac{1}{2020}\)

=>B<1

=>A>B

Ta có :

B = \(\dfrac{1}{2020}+\dfrac{2}{2019}+\dfrac{3}{2018}+...+\dfrac{2019}{2}+\dfrac{2020}{1}\)

B = \(\left(\dfrac{1}{2020}+1\right)+\left(\dfrac{2}{2019}+1\right)+\left(\dfrac{3}{2018}+1\right)+...+\left(\dfrac{2019}{2}+1\right)+1\)

B = \(\dfrac{2021}{2020}+\dfrac{2021}{2019}+\dfrac{2021}{2018}+...+\dfrac{2021}{2}+1\)

B = \(2021\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2019}+...+\dfrac{1}{2}\right)\)  (1)

Mà A = \(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\)   (2)

Từ (1) và (2) \(\Rightarrow\) \(\dfrac{A}{B}=\dfrac{1}{2021}\)

Ta có: \(B=\dfrac{1}{2020}+\dfrac{2}{2019}+\dfrac{3}{2018}+...+\dfrac{2019}{2}+\dfrac{2020}{1}\)

\(=\left(\dfrac{1}{2020}+1\right)+\left(\dfrac{2}{2019}+1\right)+\left(\dfrac{3}{2018}+1\right)+...+\left(\dfrac{2019}{2}+1\right)+1\)

\(=\dfrac{2021}{2020}+\dfrac{2021}{2019}+\dfrac{2021}{2018}+...+\dfrac{2021}{2}+\dfrac{2021}{2021}\)

Suy ra: \(\dfrac{A}{B}=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}}{2021\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\right)}=\dfrac{1}{2021}\)

Giải:

Ta có:

\(B=\dfrac{1}{2020}+\dfrac{2}{2019}+\dfrac{3}{2018}+...+\dfrac{2019}{2}+\dfrac{2020}{1}\) 

\(B=1+\left(\dfrac{1}{2020}+1\right)+\left(\dfrac{2}{2019}+1\right)+\left(\dfrac{3}{2018}+1\right)+...+\left(\dfrac{2019}{2}+1\right)\) 

\(B=\dfrac{2021}{2021}+\dfrac{2021}{2020}+\dfrac{2021}{2019}+\dfrac{2021}{2018}+...+\dfrac{2021}{2}\) 

\(B=2021.\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2019}+\dfrac{1}{2018}+...+\dfrac{1}{2}\right)\) 

\(\Rightarrow\dfrac{A}{B}=\dfrac{\left[2021.\left(\dfrac{1}{2021}+\dfrac{1}{2020}+\dfrac{1}{2019}+\dfrac{1}{2018}+...+\dfrac{1}{2}\right)\right]}{\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2021}\right)}=2021\) 

Vậy \(\dfrac{A}{B}=2021\)

a: \(=\dfrac{3}{2}\left(-21-\dfrac{1}{3}+1+\dfrac{1}{3}\right)=\dfrac{3}{2}\cdot\left(-20\right)=-30\)

b: \(=\dfrac{2018}{2019}\left(13-13-\dfrac{2018}{2019}-\dfrac{1}{2019}\right)=-\dfrac{2018}{2019}\)

Lời giải:

Xét số hạng tổng quát:

\(\frac{1}{(n+1)\sqrt{n}+n\sqrt{n+1}}=\frac{1}{\sqrt{n(n+1)}(\sqrt{n+1}+\sqrt{n})}\)

\(=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n(n+1)}(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}\)

\(=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n(n+1)}(n+1-n)}=\frac{\sqrt{n+1}-\sqrt{n}}{\sqrt{n(n+1)}}\)

\(=\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\)

Do đó:

\(S=\frac{1}{\sqrt{1}}-\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2018}}-\frac{1}{\sqrt{2019}}\)

\(=1-\frac{1}{\sqrt{2019}}\)

a: \(A=1-\dfrac{2\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}{4\left(25-\dfrac{2}{2018}+\dfrac{1}{2019}-\dfrac{1}{2020}\right)}\)

=1-2/4=1/2

b: \(B=\dfrac{5^{10}\cdot7^3-5^{10}\cdot7^4}{5^9\cdot7^3+5^9\cdot7^3\cdot2^3}\)

\(=\dfrac{5^{10}\cdot7^3\left(1-7\right)}{5^9\cdot7^3\left(1+2^3\right)}=5\cdot\dfrac{-6}{9}=-\dfrac{10}{3}\)

c: x-y=0 nên x=y

\(C=x^{2020}-x^{2020}+y\cdot y^{2019}-y^{2019}\cdot y+2019\)

=2019

Giải:

Đặt: \(A=1+2+2^2+2^3+...+2^{2018}\)

\(\Leftrightarrow A=2+2^2+2^3+2^4...+2^{2019}\)

\(\Leftrightarrow2A-A=2^{2019}-1\)

Đặt A và tử của B, ta được:

\(B=\dfrac{2^{2019}-1}{1-2^{2019}}\)

\(\Leftrightarrow B=-1\)

Vậy ...

1.

Đặt biểu thức là $A$

Ta thấy:

$\frac{1}{1+\sqrt{2}}=\frac{\sqrt{2}-1}{(1+\sqrt{2})(\sqrt{2}-1)}=\frac{\sqrt{2}-1}{2-1}=\sqrt{2}-1$

Tương tự với các phân số còn lại và công theo vế thì:

$A=(\sqrt{2}-1)+(\sqrt{3}-\sqrt{2})+...+(\sqrt{2019}-\sqrt{2018})$

$=\sqrt{2019}-1$

2.

$\sqrt{8-2\sqrt{15}}=\sqrt{5-2\sqrt{5.3}+3}+\sqrt{3-2\sqrt{3.1}+1}$

$=\sqrt{(\sqrt{5}-\sqrt{3})^2}+\sqrt{(\sqrt{3}-1)^2}$

$=|\sqrt{5}-\sqrt{3}|+|\sqrt{3}-1|$

$=\sqrt{5}-\sqrt{3}+\sqrt{3}-1=\sqrt{5}-1$

Ta có : \(\dfrac{2017+2018}{2018+2019}=\dfrac{2017}{2018+2019}+\dfrac{2018}{2018+2019}\)

Rõ ràng ta thấy : \(\dfrac{2017}{2018}>\dfrac{2017}{2018+2019}\) (1)

\(\dfrac{2018}{2019}>\dfrac{2018}{2018+2019}\) (2)

Từ (1) và (2), suy ra :

\(\dfrac{2017}{2018}+\dfrac{2018}{2019}>\dfrac{2017+2018}{2018+2019}\)

Vậy ......................

~ Học tốt ~

Ta có : \(\dfrac{2017}{2018}+\dfrac{2018}{2019}+\dfrac{2019}{2020}=\left(1-\dfrac{1}{2018}\right)+\left(1-\dfrac{1}{2019}\right)+\left(1-\dfrac{1}{2020}\right)\)\(=\left(1+1+1\right)-\left(\dfrac{1}{2018}+\dfrac{1}{2019}+\dfrac{1}{2020}\right)\)

\(=3+\left(\dfrac{1}{2018}+\dfrac{1}{2019}+\dfrac{1}{2020}\right)< 3\)

Vậy \(\dfrac{2017}{2018}+\dfrac{2018}{2019}+\dfrac{2019}{2020}< 3\)