Cho ∆𝐴𝐵𝐶 có 𝐴𝐵 = 7, 𝐵𝐶 = 25, trung tuyến 𝐴𝐷 = 12,5. Tính 𝐴𝐶

Những câu hỏi liên quan
Cho ∆𝐴𝐵𝐶 có 𝐻 là trực tâm, 𝐺 là trọng tâm. Các đường thẳng vuông góc với 𝐴𝐵 tại 𝐵 và 𝐴𝐶 tại 𝐶 cắt nhau ở 𝐷. Gọi 𝐸, 𝐹, 𝐼, 𝐽 là trung điểm của các đoạn thẳng 𝐵𝐶, 𝐴𝐷, 𝐴𝐺, 𝐻𝐺.a) Chứng minh rằng tứ giác 𝐵𝐻𝐶𝐷 là hình bình hành.b) Biết 𝐵𝐴𝐶 ̂ 60^𝑜, tính số đo góc 𝐵𝐻𝐶 ̂.c) Chứng minh rằng 𝐻, 𝐸, 𝐷 thẳng hàng.d) Chứng minh rằng 𝐴𝐻 2𝐹𝐸 và 𝐹𝐸 ⊥ 𝐵𝐶.e) Chứng minh rằng 𝐴𝐻 2𝐼𝐽 và 𝐻, 𝐺, 𝐹 thẳng hàng.
Đọc tiếp
Cho ∆𝐴𝐵𝐶 có 𝐻 là trực tâm, 𝐺 là trọng tâm. Các đường thẳng vuông
góc với 𝐴𝐵 tại 𝐵 và 𝐴𝐶 tại 𝐶 cắt nhau ở 𝐷. Gọi 𝐸, 𝐹, 𝐼, 𝐽 là trung điểm của
các đoạn thẳng 𝐵𝐶, 𝐴𝐷, 𝐴𝐺, 𝐻𝐺.
a) Chứng minh rằng tứ giác 𝐵𝐻𝐶𝐷 là hình bình hành.
b) Biết 𝐵𝐴𝐶 ̂ = 60^𝑜, tính số đo góc 𝐵𝐻𝐶 ̂.
c) Chứng minh rằng 𝐻, 𝐸, 𝐷 thẳng hàng.
d) Chứng minh rằng 𝐴𝐻 = 2𝐹𝐸 và 𝐹𝐸 ⊥ 𝐵𝐶.
e) Chứng minh rằng 𝐴𝐻 = 2𝐼𝐽 và 𝐻, 𝐺, 𝐹 thẳng hàng.
a: Xét tứ giác BHCD có
CH//BD
BH//CD
Do đó: BHCD là hình bình hành
Đúng 0
Bình luận (0)
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴 với 𝐴𝐵 = 3 𝑐𝑚; 𝐴𝐶 = 4 𝑐𝑚; vẽ đường cao 𝐴𝐸. a Chứng minh ∆𝐴𝐵𝐶 đồng dạng với ∆𝐸𝐵𝐴. b Chứng minh 𝐴𝐵² = 𝐵𝐸. 𝐵𝐶. c Tia phân giác của góc 𝐴𝐵𝐶 cắt 𝐴𝐶 tại 𝐹. Tính độ dài 𝐴𝐹.
a: Xet ΔABC và ΔEBA có
góc BAC=góc BEA
góc B chung
=>ΔABC đồng dạng với ΔEBA
b: ΔABC vuông tại A có AE vuông góc BC
nên AB^2=BE*BC
c: BF là phân giác
=>AF/AB=CF/BC
=>AF/3=FC/5=4/8=1/2
=>AF=1,5cm
Đúng 2
Bình luận (0)
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴, có 𝐴𝐵 9 𝑐𝑚; 𝐴𝐶 12 𝑐𝑚. Tia phân giác góc 𝐴 cắt 𝐵𝐶 tại 𝐷, từ 𝐷 kẻ 𝐷𝐸 vuông góc với 𝐴𝐶 (𝐸 ∈ 𝐴𝐶). a Tính tỉ số𝐵𝐷/CD Chứng minh: ∆𝐴𝐵𝐶 ∽ ∆𝐸𝐷𝐶.
Đọc tiếp
Cho tam giác 𝐴𝐵𝐶 vuông tại 𝐴, có 𝐴𝐵 = 9 𝑐𝑚; 𝐴𝐶 = 12 𝑐𝑚. Tia phân giác góc 𝐴 cắt 𝐵𝐶 tại 𝐷, từ 𝐷 kẻ 𝐷𝐸 vuông góc với 𝐴𝐶 (𝐸 ∈ 𝐴𝐶). a Tính tỉ số𝐵𝐷/CD Chứng minh: ∆𝐴𝐵𝐶 ∽ ∆𝐸𝐷𝐶.
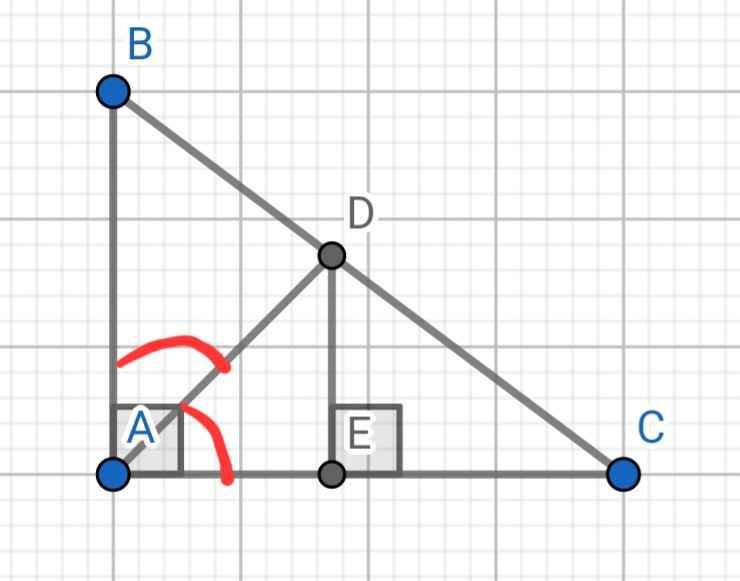
a) Do AD là đường phân giác của ∠BAC
⇒ BD/CD = AB/AC = 9/12 = 3/4
b) Xét hai tam giác vuông: ∆ABC và ∆EDC có:
∠C chung
⇒ ∆ABC ∽ ∆EDC (g-g)
Đúng 1
Bình luận (0)
a: BD/CD=AB/AC=3/4
b: Xét ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC
Đúng 1
Bình luận (0)
Cho ∆𝐴𝐵𝐶 có trung tuyến 𝐴𝐷, trọng tâm 𝐺. Qua 𝐺 kẻ đường thẳng 𝑑 cắt các cạnh 𝐴𝐵, 𝐴𝐶. Gọi 𝐸 là trung điểm 𝐴𝐺. Gọi 𝐹, 𝐻, 𝐼, 𝐽, 𝐾 là hình chiếu của 𝐵, 𝐴, 𝐸, 𝐷, 𝐶 trên đường thẳng 𝐷. Chứng minh rằng:
a) 𝐸𝐼 = 𝐷𝐽 và 𝐷𝐽 =𝐴𝐻/2. b) 𝐵𝐹 + 𝐶𝐾 = 𝐴𝐻
Cho ∆𝐴𝐵𝐶 cân tại 𝐴, 𝐷 là trung điểm đoạn 𝐴𝐵. Qua 𝐷 đường thẳng song song với 𝐵𝐶 cắt 𝐴𝐶 tại 𝐸 và đường thẳng song song với 𝐴𝐶 cắt 𝐵𝐶 tại 𝐹. a) Chứng minh ∆𝐴𝐷𝐸;∆𝐷𝐵𝐹 là tam giác cân b) Chứng minh ∆𝐷𝐴𝐹 là tam giác cân c) Chứng minh 𝐴𝐹 ⊥ 𝐷𝐸 d) Chứng minh 𝐹 là trung điểm 𝐵𝐶.
a: Xét ΔABC có
D là trung điểm của AB
DE//BC
Do đó: E là trung điểm của AC
Xét ΔADE có AD=AE
nên ΔADE cân tại A
b: Xét ΔABC có
D là trung điểm của AB
DF//AC
Do đó: F là trung điểm của BC
Xét ΔABC có
D là trung điểm của AB
F là trung điểm của BC
Do đó: DF là đường trung bình
=>DF=AE
mà AE=AD
nên DF=AD
=>ΔADF cân tại D
c: Xét tứ giác ADFE có
DF//AE
DF=AE
Do đó: ADFE là hình bình hành
mà AD=AE
nên ADFE là hình thoi
=>AF⊥DE
Đúng 0
Bình luận (1)
Cho tam giác 𝐴𝐵𝐶: 𝐴𝐵 = 35, 𝐴𝐶 = 20, góc 𝐴 = 60 độ . a) Tính chiều cao kẻ từ đỉnh 𝐴 của tam giác 𝐴𝐵𝐶. b) Tính 𝐵𝐶. c) Kẻ đường kính 𝐵𝐷 của đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶. Tính góc 𝐵𝐷𝐶 , BD và suy ra bán kính đường tròn ngoại tiếp tam giác 𝐴𝐵𝐶.
Cho ∆𝐴𝐵𝐶 có trung tuyến 𝐴𝐷, trọng tâm 𝐺. Qua 𝐺 kẻ đường thẳng 𝑑 cắt các cạnh 𝐴𝐵, 𝐴𝐶. Gọi 𝐸 là trung điểm 𝐴𝐺. Gọi 𝐹, 𝐻, 𝐼, 𝐽, 𝐾 là hình chiếu
của 𝐵, 𝐴, 𝐸, 𝐷, 𝐶 trên đường thẳng 𝐷. Chứng minh rằng:
a) 𝐸𝐼 = 𝐷𝐽 và 𝐷𝐽 =𝐴𝐻/2
b) 𝐵𝐹 + 𝐶𝐾 = 𝐴𝐻.
Câu 1. Tính diện tích tam giác ABC trong các trường hợp sau:
a) ABC là tam giác đều có cạnh 𝐴𝐵 = 6cm.
b) ABC là tam giác vuông tại A, có 𝐴𝐵𝐶 ̂ = 30𝑜 , 𝐴𝐶 = 2𝑐𝑚.
c) ABC là tam giác cân tại A, có 𝐴𝐶 = 5𝑐𝑚, 𝐵𝐶 = 6cm.
Câu 1. Tính diện tích tam giác ABC trong các trường hợp sau:
a) ABC là tam giác đều có cạnh 𝐴𝐵 = 6cm.
b) ABC là tam giác vuông tại A, có 𝐴𝐵𝐶 ̂ = 30𝑜 , 𝐴𝐶 = 2𝑐𝑚.
c) ABC là tam giác cân tại A, có 𝐴𝐶 = 5𝑐𝑚, 𝐵𝐶 = 6cm.
a, Nửa chu vi là \(\frac{6+6+6}{2}=9cm\)
Diện tích tam giác là \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}=\sqrt{9\left(9-6\right)\left(9-6\right)\left(9-6\right)}\)
\(=\sqrt{9.3.3.3}=9\sqrt{3}\)cm2
b, Xét tam giác ABC vuông tại A
tan^B = \(\frac{AC}{AB}\Rightarrow\frac{\sqrt{3}}{3}=\frac{2}{AB}\Rightarrow AB=\frac{6\sqrt{3}}{3}=2\sqrt{3}\)cm
Diện tích tam giác là \(\frac{1}{2}AB.AC=6\sqrt{3}\)cm2
c, Dựng AH là đường cao đồng thời là đường trung tuyến do tam giác ABC cân tại A
=> HC = BC/2 = 3 cm
Theo định lí Pytago tam giác AHC vuông tại H
\(AH=\sqrt{AC^2-HC^2}=4cm\)
Diện tích tam giác ABC là : \(\frac{1}{2}AH.BC=\frac{4.6}{2}=12cm^2\)










