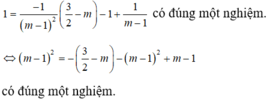cho hàm số y=\(\sqrt{X^2-2X+3}\) có đồ thị (C) và điểm A(1,a) . có bao nhiêu giá trị nguyên của a để có đúng 2 tiếp tuyến của (C) đi qua A ?

Những câu hỏi liên quan
Cho hàm số
y
x
2
-
2
x
+
3
có đồ thị (C) và điểm A(1;a). Có bao nhiêu giá trị nguyên của a để có đúng hai tiếp tuyến của (C) đi qua a? A. 3 B. 2 C. 1 D. 4
Đọc tiếp
Cho hàm số y = x 2 - 2 x + 3 có đồ thị (C) và điểm A(1;a). Có bao nhiêu giá trị nguyên của a để có đúng hai tiếp tuyến của (C) đi qua a?
A. 3
B. 2
C. 1
D. 4
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên A. 1. B. 0. C. 3. D. 4
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A( a; 1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Hỏi trong tập S có bao nhiêu giá trị nguyên
A. 1.
B. 0.
C. 3.
D. 4
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là: y= k( x-a) +1
+ Phương trình hoành độ giao điểm của d và (C) :
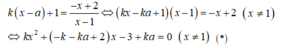
+ Với k= 0, ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
Với k≠0 , d và (C) tiếp xúc nhau khi và chỉ khi (1) có nghiệm kép
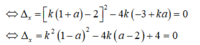
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1) vẽ được đúng tiếp tuyến thì phương trình có đúng một nghiệm k≠ 0.
*Xét 1-a= 0 hay a=1, ta có 4k+ k= 0 hạy k= -1 thỏa.
*Có f(0) = 4≠0 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là .
*Còn lại là trường hợp ∆x= 0 có nghiệm kép khi
![]()
Vậy có 2 giá trị của a thỏa mãn đầu bài là a= 1 hoặc a= 3/2.
Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
2
x
-
1
có đồ thị (C) và điểm A(a;2). Có bao nhiêu giá trị của a để có hai tiếp tuyến của (C) qua A và hai tiếp tuyến này vuông góc với nhau. A. 2. B. 1. C. 4. D. 0.
Đọc tiếp
Cho hàm số y = x 2 x - 1 có đồ thị (C) và điểm A(a;2). Có bao nhiêu giá trị của a để có hai tiếp tuyến của (C) qua A và hai tiếp tuyến này vuông góc với nhau.
A. 2.
B. 1.
C. 4.
D. 0.
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm A(a;1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng: A. 1 B.
3
2
C.
5
2...
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A(a;1). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng:
A. 1
B. 3 2
C. 5 2
D. 1 2
Đáp án B.
Pt tiếp tuyến đi qua A có dạng y=k(x-a)+1
Để có đúng 1 tiếp tuyến đi qua A thì hpt
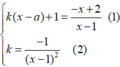
có đúng một nghiệm
Thay (2) vào (1):
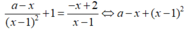
![]()
Đúng 0
Bình luận (0)
Cho hàm số
y
−
x
+
2
x
−
1
có đồ thị (C) và điểm A(a;1) Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng:...
Đọc tiếp
Cho hàm số y = − x + 2 x − 1 có đồ thị (C) và điểm A(a;1) Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng:
A. 1
B. 3/2
C. 5/2
D. 1/2
Đáp án B
Pt tiếp tuyến đi qua A có dạng y = k ( x − a ) + 1
Để có đúng 1 tiếp tuyến đi qua A thì hpt k ( x − a ) + 1 = − x + 2 x − 1 ( 1 ) k = − 1 ( x − 1 ) 2 ( 2 ) có đúng một nghiệm
Thay (2) vào (1):
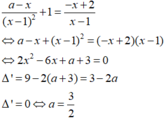
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm A ( a;1 ). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng A. 1 B.
3
2
C.
5...
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A ( a;1 ). Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) đi qua A. Tổng giá trị tất cả các phần tử của S bằng
A. 1
B. 3 2
C. 5 2
D. 1 2
Gọi phương trình tiếp tuyến là y = k( x - a ) + 1. Xét hệ phương trình.
- x + 2 x - 1 = k x - a + 1 - 1 x - 1 2 = k ⇒ 2 x 2 - 6 x + a + 3 = 0 - 1 x - 1 2 ⇒ ∆ ' = 3 - 2 a
Để có 1 tiếp tuyến thì 2 x 2 - 6 x + a + 3 = 0 có 1 nghiệm kép khác 1 hoặc có 2 nghiệm trong đó 1 nghiệm bằng 1 có
TH1. có nghiệm kép ∆ = 0 ⇔ a = 3 2
TH2. Có nghiệm bằng 1 nên a = 1. Khi đó phương trình có 2 nghiệm x =1, x= 2
Vậy S = 3 2 ; 1
Đáp án cần chọn là C
Đúng 0
Bình luận (0)
Cho hàm số
y
−
x
+
2
x
−
1
có đồ thị (C) và đi qua điểm
A
a
;
1
. Gọi S là tập tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) qua A. Tổng giá trị tất cả các phần tử của S bằng A.
5...
Đọc tiếp
Cho hàm số y = − x + 2 x − 1 có đồ thị (C) và đi qua điểm A a ; 1 . Gọi S là tập tất cả các giá trị thực của a để có đúng một tiếp tuyến của (C) qua A. Tổng giá trị tất cả các phần tử của S bằng
A. 5 2 .
B. 3 2 .
C. 1.
D. 1 2 .
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị C và điểm A( a; 1) . Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Tổng tất cả giá trị của phần tử S bằng A. 1. B. 3/2. C. 5/2. D. 1/2.
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị C và điểm A( a; 1) . Gọi S là tập hợp tất cả các giá trị thực của a để có đúng một tiếp tuyến từ C đi qua A. Tổng tất cả giá trị của phần tử S bằng
A. 1.
B. 3/2.
C. 5/2.
D. 1/2.
+ Phương trình đường thẳng d đi qua A và có hệ số góc k là : y= k ( x-a) + 1
+ Phương trình hoành độ giao điểm của d và C :
![]()
Hay kx2+ (-k-ka+2) x-3+ka=0 ( *)
+ Với k= 0 , ta có d: y= 1 là tiệm cận ngang đồ thị hàm số nên không thể tiếp xúc được.
+ Với k≠0, d và C tiếp xúc nhau khi (1) có nghiệm kép
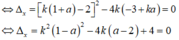
Coi đây là phương trình bậc 2 ẩn k tham số a
+ Để qua A( a; 1)vẽ được đúng tiếp tuyến thì phương trình ∆ =0 có đúng một nghiệm k≠0.
*Xét 1-a= 0 hay a=1, ta có 4k+4= 0 hay k= -1 thỏa mãn
*Có f( 0)=4 nên loại đi trường hợp có hai nghiệm trong đó có một nghiệm là 0.
*Còn lại là trường hợp ∆ x = 0 có nghiệm kép khi
![]()
Tổng là 1+ 3/2=5/2.
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
+
2
x
-
1
có đồ thị (C) và điểm
A
a
;
1
. Biết
a
m
n
(với mọi
m
,
n
∈
N
và
m...
Đọc tiếp
Cho hàm số y = - x + 2 x - 1 có đồ thị (C) và điểm A a ; 1 . Biết a = m n (với mọi m , n ∈ N và m n tối giản) là giá trị để có đúng một tiếp tuyến của (C) đi qua A. Khi đó giá trị m + n là:
A. 2
B. 7.
C. 5
D. 3.
Cho hàm số
y
−
x
+
2
x
−
1
có đồ thị (C) và điểm
A
a
;
1
.
Gọi S là tập hợp các giá trị thực của a để có đúng một tiếp tuyến của (C) kẻ qua A. Tổng giá trị các phần tử của S là: A. 1 B.
3
2...
Đọc tiếp
Cho hàm số y = − x + 2 x − 1 có đồ thị (C) và điểm A a ; 1 . Gọi S là tập hợp các giá trị thực của a để có đúng một tiếp tuyến của (C) kẻ qua A. Tổng giá trị các phần tử của S là:
A. 1
B. 3 2 .
C. 5 2 .
D. 1 2 .
Đáp án C.
Phương trình tiếp tuyến (C) tại điểm A là:
y = f ' x 0 x − x 0 + − x 0 + 2 x 0 − 1 = − 1 x 0 − 1 x − x 0 + − x 0 + 2 x 0 − 1
Do tiếp tuyến đi qua điểm A a ; 1 nên
1 = x 0 − a + 2 − x 0 x 0 − 1 x 0 − 1 2
⇔ x 0 − 2 2 = − x 0 2 + 4 x 0 − 2 − a ⇔ 2 x 0 2 − 6 x 0 + 3 + a = 0
Để đúng một tiếp tuyến đi qua A thì (*) có
nghiệm kép hoặc (*) có 2 nghiệm
phân biệt tróng đó có một nghiệm
x 0 = 1 ⇔ Δ ' = 3 − 2 a = 0 Δ ' = 3 − 2 a > 0 2.1 − 6 + 3 + a = 0 ⇔ a = 3 2 a = 1 .
Đúng 0
Bình luận (0)