Lấy thêm trung điểm K của BC rồi dùng định lý Pytago tính các cạnh MB, MC, MA theo AB, AC, BC, AK

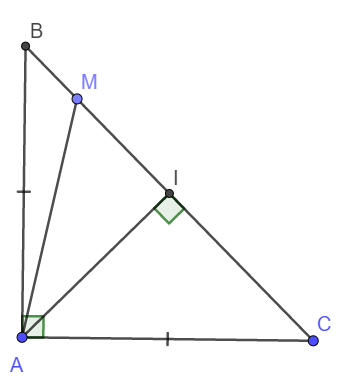
Đặt AB = AC = a \(\Rightarrow BC=\sqrt{AB^2+AC^2}=a\sqrt{2}\)

Gọi I là trung điểm BC, do tam giác ABC cân nên AI cũng là đường cao.

\(AI=BI=IC=\frac{a\sqrt{2}}{2}\)

Đặt MI = x ( 0 < x < \(\frac{a\sqrt{2}}{2}\) )

Ta có \(BM^2=\left(BI-MI\right)^2=\left(\frac{a\sqrt{2}}{2}-x\right)^2\)

\(MC^2=\left(IC+MI\right)^2=\left(\frac{a\sqrt{2}}{2}+x\right)^2\)

\(\Rightarrow MB^2+MC^2=2\left(\frac{a^2}{2}+x^2\right)=2\left(AI^2+MI^2\right)\)

\(=2AM^2\)

Vậy nên ta đã chứng minh được \(\forall M\in BC:BM^2+MC^2=2AM^2\)

Ngoài cách của cô Huyền ra, mình còn có thêm một cách như sau:

Gọi D và E lần lượt là hình chiếu của M lên AB và AC.

Xét tam giác MDB vuông tại B có \(\widehat{MBD}=45^o\)

\(\Rightarrow\)\(\Delta MDB\) vuông cân tại D

\(\Rightarrow\)\(MB^2=2MD^2\)

Tương tự ta có \(MC^2=2ME^2\)

Cộng vế theo vế ta được:

\(MB^2+MC^2=2MD^2+2ME^2\)

\(\Rightarrow\)\(MB^2+MC^2=2MA^2\left(đpcm\right)\)

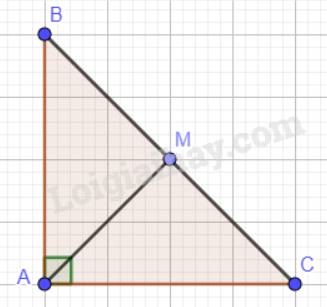
Tam giác ABC vuông cân tại A nên \(\widehat A = 90^\circ ;\widehat B = \widehat C; AB = AC\).

Tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat C = 90:2 = 45^\circ \).

Xét tam giác ABM và tam giác ACM có:

AB = AC

AM chung

BM = CM

\(\Rightarrow \Delta ABM = \Delta ACM\) (c.c.c)

\(\Rightarrow \widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng)

Mà \(\widehat {BAM} + \widehat {CAM}=\widehat{BAC}=90^0\)

\(\Rightarrow \widehat {BAM} = \widehat {CAM} = 90:2 = 45^\circ \).

Xét tam giác MAB: \(\widehat {MBA} = \widehat {BAM} = 45^\circ  \Rightarrow \widehat {BMA} = 90^\circ ;MB = MA\).

Vậy tam giác MAB vuông cân tại M.

a: BC=15cm

AM=7,5cm

Chọn đáp án C

a) Các tam giác DBA và tam giác EAC vuông cân nên \(\widehat{ABD}=\widehat{DAB}=45^o,\widehat{CAE}=\widehat{ECA}=45^o\).
\(\widehat{DAE}=\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=45^o+90^o+45^o=180^o\).
Suy ra D, A, E thẳng hàng.
b) Có M là trung điểm của BC và tam giác BAC vuông tại A nên MA = MB = MC.
Suy ra \(\Delta DBM=\Delta DAM\left(c.c.c\right)\). Vì vậy \(\widehat{BDM}=\widehat{ADM}\) hay DM là tia phân giác góc ADB.
mà tam giác BDA cân tại D nên DM cũng là đường cao hay \(DM\perp AB\).
Tương tự cho \(EM\perp AC\).
c) Theo chứng minh trên DM là tia phân giá góc ADB nên \(\widehat{BDM}=\widehat{MDA}=45^o\). Tương tự \(\widehat{AEK}=\widehat{KEC}=45^o\).
Vì vậy ta, giác DME vuông cân.
d) Do các tam giác ADB và tam giác AEC cân và DF và EK là đường cao tương ứng nên DF và EK cũng là các đường trung tuyến.
Vì vậy F và K lần lượt là trung điểm của AB và AC.
Từ đó suy ra FK là đường trung bình của tam giác BAC hay \(FK=\frac{1}{2}BC\).

 

tại sao ma=mb=mc