a: Khi m=4 thì (d): y=-x+4

PTHĐGĐ là:

1/2x^2=-x+4

=>x^2=-2x+8

=>x^2+2x-8=0

=>(x+4)(x-2)=0

=>x=2 hoặc x=-4

Khi x=2 thì y=1/2*2^2=2

Khi x=-4 thì y=1/2(-4)^2=8

Đáp án B

Lời giải:

Phương trình hoành độ giao điểm:

$\frac{-1}{4}x^2=2x+3$

$\Leftrightarrow \frac{1}{4}x^2+2x+3=0$

$\Leftrightarrow x=-2$ hoặc $x=-6$

$x=-2$ thì $y=2x+3=2(-2)+3=-1$. Giao điểm 1 là $(-2;-1)$
$x=-6$ thì $y=2x+3=2(-6)+3=-9$. Giao điểm 2 là $(-6; -9)$

Đáp án A.

Đáp án A

Xét ptr hoành độ của `(P)` và `(d)` có:

        `x^2=mx-1`

`<=>x^2-mx+1=0`   `(1)`

Để `(d)` cắt `(P)` tại `2` điểm pb thì ptr `(1)` có `2` `n_o` pb

  `=>\Delta > 0`

`<=>(-m)^2-4 > 0`

`<=>m^2 > 4`

`<=>` $\left[\begin{matrix} m > 4\\ m < -4\end{matrix}\right.$

Với `m > 4` hoặc `m < -4`, áp dụng Vi-ét có:`{(x_1+x_2=[-b]/a=-m),(x_1.x_2=c/a=1):}`

Ta có:`x_2(x_1 ^2+1)=3`

`<=>x_2(x_1 ^2+x_1.x_2)=3`

`<=>x_1.x_2(x_1+x_2)=3`

`<=>1(-m)=3`

`<=>m=-3` (ko t/m)

Vậy không có gtr nào của `m` t/m yêu cầu đề bài

a: Thay x=0 và y=-5 vào (d), ta được:

2(m+1)*0-m^2-4=-5

=>m^2+4=5

=>m=1 hoặc m=-1

b:

PTHĐGĐ là;

x^2-2(m+1)x+m^2+4=0

Δ=(2m+2)^2-4(m^2+4)

=4m^2+8m+4-4m^2-16=8m-12

Để PT có hai nghiệm phân biệt thì 8m-12>0

=>m>3/2

x1+x2=2m+2; x1x2=m^2+4

(2x1-1)(x2^2-2m*x2+m^2+3)=21

=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21

=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21

=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21

=>(2x1-1)(2x2-1)=21

=>4x1x2-2(x1+x2)+1=21

=>4(m^2+4)-2(2m+2)+1=21

=>4m^2+16-4m-4-20=0

=>4m^2-4m-8=0

=>(m-2)(m+1)=0

=>m=2(nhận) hoặc m=-1(loại)

Đáp án D

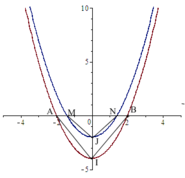
Phép tịnh tiến theo v → 0 ; b  biến parabol P : y = x 2 − 4  thành parabol  P ' : y = x 2 − 4 + b

Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là:  − 2 ; 0 , 2 ; 0

Giao điểm M,N với Ox của (P) có toạn độ lần lượt là:  − 4 − b ; 0 , 4 − b ; 0

Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt:  0 ; − 4 , 0 ; − 4 + b

Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:

I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1

Vì (d1)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)

Vậy: (d1): y=3x+b

Thay x=-2 vào (P), ta được:

\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)

Thay x=-2 và y=2 vào (d1), ta được:

\(3\cdot\left(-2\right)+b=2\)

\(\Leftrightarrow b=8\)(thỏa ĐK)

Vậy: (d1): y=3x+8

để \(\left(d1\right)\) sogn song với \(\left(d\right)\)

\(< =>\left\{{}\begin{matrix}a=3\\b\ne-4\end{matrix}\right.\)

để (d1) cắt (P) tại A có hoành độ -2\(=>x=-2\)

\(=>\dfrac{1}{2}x^2=3x+b< =>\dfrac{1}{2}\left(-2\right)^2=3\left(-2\right)+b=>b=8\left(tm\right)\) 

=>\(\left(d1\right):y=3x+8\)