Gợi ý: Gọi 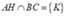, chứng minh được AK ^ BC.

Áp dụng cách làm tương tự 4A suy ra ĐPCM

Trã lời dùm

Kẻ \(HM\perp BC\)
Xét \(\Delta BHM\) và \(\Delta BCD\) ta có:
\(\widehat{BMH}=\widehat{BDC}=90^o\)
\(\widehat{CBD}\) chung
\(\Rightarrow\Delta BHM\sim\Delta BCD\left(g.g\right)\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{BH}{BC}\Rightarrow BM\times BC=BH\times BD\left(1\right)\)
Xét \(\Delta CMH\) và \(\Delta CEB\) ta có:
\(\widehat{BCE}\) chung
\(\widehat{CMH}=\widehat{CEB}=90^o\)
\(\Rightarrow\Delta CMH\sim\Delta CEB\left(g.g\right)\)
\(\Rightarrow\dfrac{CH}{CB}=\dfrac{CM}{CE}\Rightarrow CM\times CB=CH\times CE\left(2\right)\)
Cộng 2 vế của (1)(2) lại với nhau ta đc:
\(BM.BC+CM.CB=BH.BD+CH.CE\)
\(\Leftrightarrow BC\left(BM+CM\right)=BH.BD+CH.CE\)
\(\Rightarrow BC^2=BH.BD+CH.CE\left(đcpcm\right)\)
Vậy..............

bonus cho cái hình lun nek

a) Chứng minh tam giác AED đông dang tam giác ACB

b) Kẻ HI vuông góc BC

Có BHxBD+CHxCE=BC^2 bằng xét 2 cặp tam giác đông dạng.

mình cần gâps huhu

=>AM=AN

1:

a: góc AEH+góc ADH=180 độ

=>AEHD nội tiếp

b: góc BEC=góc BDC=90 độ

=>BEDC nội tiếp

c: BEDC nội tiếp

=>góc EBD=góc ECD

d: Xét ΔABC có

BD,CE là đường cao

BD cắt CE tại H

=>H là trực tâm

=>AH vuông góc BC

Cho tam giác nhọn ABC có hai đường cao BD và CE căt nhau tại H .

Chứng minh rằng : BC^2=BH.BD+CH.CE

Bài này em có thể giải như sau

1)1) Ta có:

△CDH∼△ACE (g.g)△CDH∼△ACE (g.g)

⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE⇒CHAE=CDAC⇒CH.AC=AE.CD=AB.AE

△ADH∼△ACF (g.g)△ADH∼△ACF (g.g)

⇒ADAC=AHAF⇒AH.AC=AD.AF⇒ADAC=AHAF⇒AH.AC=AD.AF

Do đó: AC2=AH.AC+CH.AC=AB.AE+AD.AFAC2=AH.AC+CH.AC=AB.AE+AD.AF

2)2) Dựng HFHF vuông góc BC.BC. Ta có:

△BFH∼△BDC△BFH∼△BDC

⇒BFBD=BHBC⇒BF.BC=BD.BH⇒BFBD=BHBC⇒BF.BC=BD.BH

△CFH∼△CEB△CFH∼△CEB

⇒CF/CE=CHCB⇒CF.BC=CE.CH⇒CFCE=CHCB⇒CF.BC=CE.CH

Do đó: BC^2=BF.BC+CF.BC=BD.BH=CE.CH

các dấu kí tự bạn tự thêm nhé