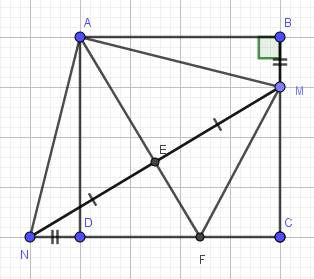
Cho hình vuông ABCD cố định, M là 1 điểm lấy trên cạnh BC(M khác B). Tia AM cắt DC tại P.Trên tia đối của tia DC lấy điểm N sao cho DN=BM
a.Chứng minh tam giác AND = tam giác ABM và tam giác MAN là tam giác vuông cân.
b.Chứng minh tam giác ABM và tam giác PDA đồng dạng và BC2=BM.DP
c.Qua A vẽ đường thẳng vuông góc với MN tại H và cắt CD tại Q,MN cắt AD ở I.Chứng minh AH.AQ=AI.AD và góc DAQ= góc HMQ
d.Chứng minh tam giác NDH và tam giác NIQ đồng dạng