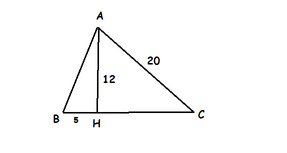
Cho tam giác nhọn ABC, kẻ \(AH\perp BC\). Tính chu vi tam giác ABC biết \(AC=20cm,AH=12cm,BH=5cm\)

Những câu hỏi liên quan
Cho tam giác ABC nhọn .kẻ AH vuông góc với BC .Tính chu vi tam giác ABC biết AC=20cm,AH=12cm,BH=5cm
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
chu vi là 54 cm
\(\Delta ABH\)vuông tại H \(\Rightarrow AH^2+BH^2=AB^2\)( định lý Pytago )
mà \(AH=12cm\), \(BH=5cm\)
\(\Rightarrow12^2+5^2=AB^2\)\(\Rightarrow AB^2=144+25\)
\(\Rightarrow AB^2=169\)\(\Rightarrow AB=13\)( cm )
\(\Delta AHC\)vuông tại H \(\Rightarrow AH^2+HC^2=AC^2\)( định lý Pytago )
\(\Rightarrow HC^2=AC^2-AH^2\)
mà \(AC=20cm\); \(AH=12cm\)
\(\Rightarrow HC^2=20^2-12^2\)\(\Rightarrow HC^2=400-144\)
\(\Rightarrow HC^2=256\)\(\Rightarrow HC=16\)( cm )
mà \(BC=HB+HC\)\(\Rightarrow BC=5+16=21\)( cm )
\(\Rightarrow P_{ABC}=AB+AC+BC=13+20+21=54\)( cm )
Vậy chu vi của \(\Delta ABC\)là 54 cm
cho tam giác nhọn ABC kẻ AH vuông góc với BC . tính chu vi của tam giác ABC biết AC=20cm AH=12cm BH=5cm
cho tam giác ABC nhọn, AH vuông BC biết AC=20cm ; AH=12cm ; BH=5cm. Tính chu vi tam giác ABC
\(AB^2=AH^2+BH^2\)
\(AB=12^2+5^2=169\)
\(AB=\sqrt{169}=13\left(cm\right)\)
▲AHC vuông tại H ta có:
HC\(^2\)=\(AC^2-AH^2\)=\(20^2-12^2\)=256
\(\)Chu vi ▲ABC là:
AB+BC+AC=AB+BH+HC+AC=\(13+5+16+20=54\left(cm\right)\)
Đúng 2
Bình luận (0)
Tham khảo:
Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)
Đúng 2
Bình luận (0)
Ta có : \(\Delta ABH\) vuông tại H
Theo đl pytago ta có : \(AH^2+BH^2=AB^2\)
-> \(AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
\(\Delta ACH\) vuông tại H
Theo đl pytago ta có : \(AC^2-AH^2=CH^2\)
-. \(CH=\sqrt{20^2-12^2}=16\left(cm\right)\)
Chu vi \(\Delta ABC=AB+AC+BC=13+20+16+5=54\left(cm\right)\)
Đúng 1
Bình luận (0)
cho tam giác ABC nhọn đường cao AH (H thuộc BC)tính chu vi tam giác ABC,biết AC=20cm, AH=12cm và BH=5cm
\(HC=\sqrt{AC^2-AH^2}=16\left(cm\right)\)
BC=BH+HC=21(cm)
\(AB=\sqrt{AH^2+HB^2}=13\left(cm\right)\)
C=AB+BC+AC=13+20+21=54(cm)
Đúng 2
Bình luận (0)
Xét tam giác vuông AHB có
AH ^2 + BH ^2 = AB ^2 ( Pytago)
=> AB ^2 = 12^2 + 5^2
=> Ab = 13
Xét tam giác vuông AHC có
AH^2 + HC^2 = AC ^2 ( Pytago)
=> HC^2 = AC^2 - AH^2 = 20^2 -12^2
=> HC =16
BC = HC + BH = 16 + 5 = 21
Chu vi tam giác ABC là AB + AC + BC = 13 + 20 + 21= 54 cm
Đúng 0
Bình luận (0)
cho tam giác nhọn abc kẻ ah vuông góc với bc biết ac=20cm ah=12cm bh=16cm tính chu vi tam giác abc
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+BH^2\)
\(\Leftrightarrow AB^2=12^2+16^2=400\)
hay AB=20(cm)
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow HC^2=AC^2-AH^2=20^2-12^2=256\)
hay HC=16(cm)
Ta có: BH+HC=BC(H nằm giữa B và C)
nên BC=16+16=32(cm)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+BC+AC=20+32+20=72\left(cm\right)\)
Đúng 1
Bình luận (0)
Lời giải:
Áp dụng định lý Pitago cho tam giác $AHC$ vuông tại $H$:
$HC=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=16$ (cm)
Áp dụng định lý Pitago cho tam giác $AHB$ vuông tại $H$:
$AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20$ (cm)
Chu vi tam giác $ABC$:
$AB+BC+AC=AB+BH+CH+AC=20+16+16+20=72$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác abc nhọn AH vuông BC (H thuộc BC). Biết AC=20cm,AH=12cm,BH=5cm
A) tính chu vi tam giác abc
B) tính diện tích tam giác abc
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC= 20cm, AH = 12 cm và BH = 5cm
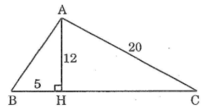
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AC = 20, AH = 12cm, BH = 5cm ?
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.
Đúng 0
Bình luận (0)
Xét ΔΔAHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = √256256 = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét ΔΔAHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = √169169 = 13 (cm)
Chu vi của ΔΔABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của ΔΔABC là 54 cm.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 3: Cho tam giác ABC nhọn. Kẻ AH vuông góc với BC. Biết AC = 20cm; AH = 12cm; HB = 5cm a/ Tính độ dài cạnh AB b/ Tính chu vi tam giác ABC
a) Xét ΔAHB vuông tại H áp dụng định lý Py-ta-go ta có:
\(AB^2=AH^2+HB^2\)
\(\Rightarrow AB=\sqrt{AH^2+HB^2}\)
\(\Rightarrow AB=\sqrt{12^2+5^2}=13\left(cm\right)\)
b) Xét ΔAHC vuông tại H áp dụng định lý Py-ta-go ta có:
\(AC^2=AH^2+HC^2\)
\(\Rightarrow HC=\sqrt{AC^2-AH^2}\)
\(\Rightarrow HC=\sqrt{20^2-12^2}=16\left(cm\right)\)
\(\Rightarrow BC=HB+HC=5+16=21\left(cm\right)\)
\(\Rightarrow C_{ABC}=BC+AB+AC=21+13+20=54\left(cm\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC nhọn . Kẻ AH vuông góc với BC. Tính chu vi tam giác ABC biết AH= 12cm;BH=5cm;CH=16cm
































