Giá trị nhỏ nhất của hàm số y= 5cos2x - 12sin2x là
A. 17
B. -17
C. -7
D. -13
Cho hàm số y = f(x) = 3x2 – 5. Giá trị f(–2) bằng A. -17 B. 7 C. -7 D. 17
Thay giá trị -2 vào hàm số ta được :
\(3.\left(-2\right)^2-5=3.\left(-4\right)-5=-17\)
tìm giá trị nhỏ nhất hoặc giá trị lớn nhất của các biểu thức sau
a)A=x2-6x+13
b)B=2x2+16x-17
c)C=4x-x2
d)D=x2-4xy+5y2+6y+17
a) A = x2 - 6x + 13 = x2 - 2.x.3 + 33 +4 = (x-3)2 + 4 >= 4 suy ra minA=4
mấy câu kia giải tương tự
Tìm x để
a)A=\(\frac{13}{17-x}\)đạt giá trị lớn nhất
b)B=\(\frac{13}{x-7}\)đạt giá trị nhỏ nhất
c)C=\(\frac{40-3x}{13-x}\)đạt giá trị lớn nhất
d)D=\(\frac{20-x}{x-12}\)đạt giá trị nhỏ nhất
Giải các phương trình sau: a) cosx – √3sinx = √2; b) 3sin3x – 4cos3x = 5; c) 2sin2x + 2cos2x – √2 = 0; d) 5cos2x + 12sin2x -13 = 0.
a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2 ⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3 ⇔ cos(x +π/3) = √2/2 ⇔ b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1. Đặt α = arccos thì phương trình trở thành cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π ⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5). c) Ta có sinx + cosx = √2cos(x – π/4) nên phương trình tương đương với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2 ⇔ d) 5cos2x + 12sin2x -13 = 0 ⇔ Đặt α = arccos5/13 thì phương trình trở thành cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1 ⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).
Giải phương trình sau: 5cos2x + 12sin2x - 13 = 0
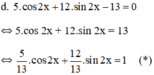
Vì 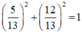 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn
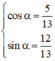
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
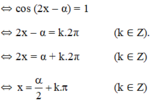
Vậy phương trình có họ nghiệm
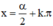 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 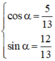
Tìm giá trị nhỏ nhất của các biểu thức sau với x là số nguyên :
a ) A = \(\frac{17}{x-13}\)
b ) B = \(\frac{17-x}{x-11}\)
a, Ta có : x-13\(\ne0\)
Mà để phân số A có giá trị nhỏ nhất => A=1
=> 17/x-13=1
=> x-13=17
=> x=30
:)
đúng sai làm thì bieets
1. Tìm các số x, y, z thuộc N* biết x/7 + y/11 + z/13 = 0,(946053)
2. CMR: -0,7(4343 - 1717) là một số nguyên
3. Cho 4 số không âm a, b, c, d thỏa mãn a + b + c+ d. Gọi S là tổng các giá trị tuyệt đói của hiệu từng cặp số có được từ 4 số này. Tìm GTLN của S.
Dùng chương trình lớp 7 học kì 1 nha!
Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức:
a) A = (x - 2)2 + (y + 1)2 + 1 b) B = 7 - (x + 3)2
c) C = |2x - 3| - 13 d) D = 11 - |2x - 13|
dúp :(
\(a.A=\left(x-2\right)^2+\left(y+1\right)^2+1\ge1\forall x;y\) . " = " \(\Leftrightarrow x=2;y=-1\)
b.\(B=7-\left(x+3\right)^2\le7\forall x\) " = " \(\Leftrightarrow x=-3\)
c.\(C=\left|2x-3\right|-13\ge-13\forall x\) " = " \(\Leftrightarrow x=\dfrac{3}{2}\)
d.\(D=11-\left|2x-13\right|\le11\forall x\) " = " \(\Leftrightarrow x=\dfrac{13}{2}\)
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?

A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)