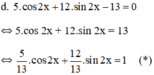
Vì 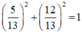 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn
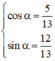
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
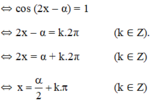
Vậy phương trình có họ nghiệm
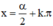 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 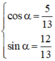
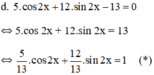
Vì 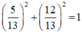 nên tồn tại α thỏa mãn
nên tồn tại α thỏa mãn
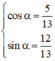
(*) ⇔ cos α.cos 2x + sin α. sin 2x = 1
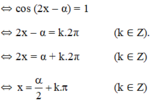
Vậy phương trình có họ nghiệm
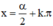 (k ∈ Z)
(k ∈ Z)
với α thỏa mãn 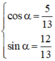
Giải phương trình c o t x - 1 = cos 2 x 1 + tan x + sin 2 x - 1 2 sin 2 x
Tổng các nghiệm của phương trình cos4x+ 12 sin 2 x - 1 = 0 trong khoảng - π ; 3 π là:
A. x = k π
B. x = 2 π
C. x = 3 π
D. x = 3 π 2
Giải phương trình f′(x) = g(x), biết rằng f ( x ) = 1 2 sin 2 x + 5 cos x , g ( x ) = 3 sin 2 x + 3 1 + tan 2 x
Phương trình sin x + cos x = 1 - 1 2 sin 2 x có nghiệm là:
A. x = π 6 + k π 2 h o ặ c x = k π 4 , k ∈ ℤ
B. x = π 8 + k π 2 h o ặ c x = k π 2 , k ∈ ℤ
C. x = π 4 + k π h o ặ c x = k π , k ∈ ℤ
D. x = π 2 + k 2 π h o ặ c x = k 2 π , k ∈ ℤ
Giải phương trình sau: c o t 2 x 2 = 1 3
2sinxcosx+ 5cos2x -4 = 0
Giải phương trình sau: cos2x.tanx = 0
Giải phương trình sau: cotx = 0
Giải phương trình sau: tanx = 0