Cho \(\Delta\)ABC, tia phân giác của \(\widehat{BAC}\) cắt cạnh BC tại D. Lấy M và N là 2 điểm nằm giữa A và D sao cho \(\widehat{ABM}\) = \(\widehat{CBN}\) ( M khác N). So sánh \(\widehat{ACM}\) với \(\widehat{BCN}\)

Những câu hỏi liên quan
Cho tam giác ABC có widehat{B}widehat{C}; tia phân giác của góc A cắt BC tại M. Trên tia đối của tia MA lấy điểm D sao MD MA. a) Chứng minh: Delta ABMDelta ACM b) Chứng minh: BC vuông góc với AM. c) Chứng minh: AB // CD .d) Cho biết, nếuwidehat{ACB}55^o, tính số đowidehat{MDC} .
Đọc tiếp
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\); tia phân giác của góc A cắt BC tại M. Trên tia đối của tia MA lấy điểm D sao MD = MA.
a) Chứng minh: \(\Delta ABM=\Delta ACM\)
b) Chứng minh: BC vuông góc với AM.
c) Chứng minh: AB // CD .
d) Cho biết, nếu\(\widehat{ACB}=55^o\), tính số đo\(\widehat{MDC}\) .
a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
Đúng 1
Bình luận (0)
Bài 1: Cho tam giác ABC, các tia phân giác của góc B, C cắt nhau tại Ia) Trong tam giác BIC, cạnh nào là cạnh lớn nhất?b) Nếu có IB IC, hãy so sánh cạnh AB và ACBài 2: Cho tam giác ABC đều. Điểm M thuộc cạnh BC sao cho BM dfrac{1}{3}BC. Gọi N là trung điểm của MCa) Chứng minh △ABM △CANb) So sánh AB và ANc) Trên tia đối của AM lấy điểm D sao cho M là trung điểm của AD. So sánh widehat{DAN} và widehat{ADN}d) Chứng minh rằng widehat{BAM} 20^{o}
Đọc tiếp
Bài 1: Cho tam giác ABC, các tia phân giác của góc B, C cắt nhau tại I
a) Trong tam giác BIC, cạnh nào là cạnh lớn nhất?
b) Nếu có IB < IC, hãy so sánh cạnh AB và AC
Bài 2: Cho tam giác ABC đều. Điểm M thuộc cạnh BC sao cho BM = \(\dfrac{1}{3}\)BC. Gọi N là trung điểm của MC
a) Chứng minh △ABM = △CAN
b) So sánh AB và AN
c) Trên tia đối của AM lấy điểm D sao cho M là trung điểm của AD. So sánh \(\widehat{DAN}\) và \(\widehat{ADN}\)
d) Chứng minh rằng \(\widehat{BAM}\) < \(20^{o}\)
Bài 2: Em tham khảo bài tương tự tại đây nhé.
Câu hỏi của Dang Khanh Ngoc - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho Delta ABC nhọn, AB AC , tia phân giác của widehat{BAC} cắt cạnh BC tại E. Trên cạnh AC lấy điểm F sao cho AFAB.a) Chứng minh: Delta AEBDelta AEF b) M là giao điểm của BF và AE. Chứng minh: MB MC, AE perp BF tại Mc) Trên tia AB lấy điểm D sao cho AD AC. Gọi K là trung điểm của CD. Chứng minh: 3 điểm A, E, K thẳng hàng.
Đọc tiếp
Cho \(\Delta ABC\) nhọn, \(AB< AC\) , tia phân giác của \(\widehat{BAC}\) cắt cạnh \(BC\) tại \(E\). Trên cạnh \(AC\) lấy điểm \(F\) sao cho \(AF=AB\).
a) Chứng minh: \(\Delta AEB=\Delta AEF\)
b) M là giao điểm của BF và AE. Chứng minh: MB = MC, AE \(\perp\) BF tại M
c) Trên tia AB lấy điểm D sao cho AD = AC. Gọi K là trung điểm của CD. Chứng minh: 3 điểm A, E, K thẳng hàng.
a: Xét ΔAEB và ΔAEF có
AE chung
\(\widehat{BAE}=\widehat{FAE}\)
AB=AF
Do đó: ΔAEB=ΔAEF
b: Sửa đề: Chứng minh MB=MF
Ta có: ΔABE=ΔAFE
=>AB=AF
=>ΔABF cân tại A
Ta có: ΔABF cân tại A
mà AM là đường phân giác
nên M là trung điểm của BF và AM\(\perp\)BF
M là trung điểm của BF nên MB=MF
AM\(\perp\)BF tại M
=>AE\(\perp\)BF tại M
c: ta có: ΔABE=ΔAFE
=>\(\widehat{ABE}=\widehat{AFE}\)
Ta có: \(\widehat{ABE}+\widehat{DBE}=180^0\)(hai góc kề bù)
\(\widehat{AFE}+\widehat{CFE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABE}=\widehat{AFE}\)
nên \(\widehat{EBD}=\widehat{EFC}\)
Ta có: AB+BD=AD
AF+FC=AC
mà AB=AF và AD=AC
nên BD=FC
Xét ΔEBD và ΔEFC có
EB=EF
\(\widehat{EBD}=\widehat{EFC}\)
BD=FC
Do đó: ΔEBD=ΔEFC
=>ED=EC
=>E nằm trên đường trung trực của DC(1)
ta có: AD=AC
=>A nằm trên đường trung trực của DC(2)
Ta có: KD=KC
=>K nằm trên đường trung trực của DC(3)
Từ (1),(2),(3) suy ra A,E,K thẳng hàng
Đúng 2
Bình luận (1)
Cho Delta ABC có AB AC. D là trung điểm của BC.a) Chứng minh: Delta ADB Delta ADC và AD là tia phân giác của widehat{BAC}.b) Vẽ DCperp AD tại M. Trên cạnh Ac lấy điểm N sao cho AN AM. Chứng minh: Delta AMD Delta AND và DCperp AN.c) Gọi K là trung điểm của NC. Trên tia DK lấy điểm E sao cho K là trung điểm của DE. Chứng minh: Delta KCD Delta KNE.d) Chứng minh: MN // BC và 3 điểm M, N, E thẳng hàng.
Đọc tiếp
Cho \(\Delta ABC\) có AB = AC. D là trung điểm của BC.
a) Chứng minh: \(\Delta ADB\) = \(\Delta ADC\) và AD là tia phân giác của \(\widehat{BAC}\).
b) Vẽ \(DC\perp AD\) tại M. Trên cạnh Ac lấy điểm N sao cho AN = AM. Chứng minh: \(\Delta AMD\) = \(\Delta AND\) và \(DC\perp AN\).
c) Gọi K là trung điểm của NC. Trên tia DK lấy điểm E sao cho K là trung điểm của DE. Chứng minh: \(\Delta KCD\) = \(\Delta KNE\).
d) Chứng minh: MN // BC và 3 điểm M, N, E thẳng hàng.
a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
b: Sửa đề: DM\(\perp\)AB tại M. Chứng minh AC\(\perp\)DN
Xét ΔAMD và ΔAND có
AM=AN
\(\widehat{MAD}=\widehat{NAD}\)
AD chung
Do đó: ΔAMD=ΔAND
=>\(\widehat{AMD}=\widehat{AND}\)
mà \(\widehat{AMD}=90^0\)
nên \(\widehat{AND}=90^0\)
=>DN\(\perp\)AC
c: Xét ΔKCD và ΔKNE có
KC=KN
\(\widehat{CKD}=\widehat{NKE}\)(hai góc đối đỉnh)
KD=KE
Do đó: ΔKCD=ΔKNE
d: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Ta có: ΔKCD=ΔKNE
=>\(\widehat{KCD}=\widehat{KNE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NE//DC
=>NE//BC
ta có: NE//BC
MN//BC
NE,MN có điểm chung là N
Do đó: M,N,E thẳng hàng
Đúng 1
Bình luận (0)
Cho tam giác ABC có \(\widehat{B}=\widehat{C}\). Tia phân giác của \(\widehat{B}\) cắt AC ở M và tia phân giác của \(\widehat{C}\) cắt AB ở N.
a) So sánh BM và CN;
b) Chứng minh: \(\Delta ABM=\Delta ACN\).
Bài này mình thấy chứng minh phần b trước thì ra phần a luôn =)))
b)Tam giác ABC có 2 góc bằng nhau: \(\widehat{ABC}=\widehat{ACB}\) =>Tam giác ABC cân tại A => AB=AC (1)
Tia BM là tia phân giác của góc ABC => \(\widehat{ABM}=\widehat{BM}C=\frac{1}{2}.\widehat{ABC}\)
Tia CN là tia phân giác của góc ACB => \(\widehat{ACN}=\widehat{NCB}=\frac{1}{2}.\widehat{ACB}\)
Mà \(\widehat{ABC}=\widehat{ACB}\) <=> \(\frac{1}{2}.\widehat{ABC}=\frac{1}{2}.\widehat{ACB}\) => \(\widehat{ABM}\)\(=\widehat{ACN}\) (2)
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(\widehat{BAC}\) là góc chungAB=AC (suy ra ở (1))\(\widehat{ABM}\)\(=\widehat{ACN}\) (suy ra ở (2))=>\(\Delta ABM\)=\(\Delta ACN\) (g.c.g) (đpcm)a)Theo chứng minh phần b ta có:\(\Delta ABM\)=\(\Delta ACN\) => BM=CN (2 cạnh tương ứng)
Đúng 0
Bình luận (0)
ChoDelta ABC cân tại A , cạnh đáy nhỏ hơn cạnh bên. Từ trung điểm I của đoạn thẳng AC kẻ đường vuông góc với AC cắt đường thẳng BC tại M. TRên tia đối của tia AM lấy điểm N sao cho AN BM.a, Chứng minh : widehat{AMC}widehat{BAC}b, Chứng minh: CM CNc, Muốn cho CM CN thì tam giác cân ABC cho trước phải có thêm điều kiện gì ?
Đọc tiếp
Cho\(\Delta ABC\) cân tại A , cạnh đáy nhỏ hơn cạnh bên. Từ trung điểm I của đoạn thẳng AC kẻ đường vuông góc với AC cắt đường thẳng BC tại M. TRên tia đối của tia AM lấy điểm N sao cho AN = BM.
a, Chứng minh : \(\widehat{AMC}=\widehat{BAC}\)
b, Chứng minh: CM = CN
c, Muốn cho CM CN thì tam giác cân ABC cho trước phải có thêm điều kiện gì ?
1) Cho Delta ABC có ABAC. Lấy điểm O nằm trong Delta ABCsao cho OBOC.Gọi M là trung điểm của BC a) CM widehat{B}widehat{C}b) CM : AO là tia phân giác củawidehat{BAC}c) CM: A,O,M thẳng hàngd) CM : AOperpBCe) AM là đường trung trực của BC2) Cho widehat{PQR}có widehat{Q}widehat{R}. Vẽ tia phân giác PM ( Min QR) a) CM : widehat{PMR}-widehat{PMQ}widehat{PQR}-widehat{R}b) Đường thẳng chứa tia phân giác góc ngoài tại đỉnh P của Delta PQRcắt đường thẳng QR tại N. Cm 2widehat{PNQ}widehat{PQR}-widehat{R}
Đọc tiếp
1) Cho \(\Delta ABC\) có AB=AC. Lấy điểm O nằm trong \(\Delta ABC\)sao cho OB=OC.Gọi M là trung điểm của BC
a) CM \(\widehat{B}=\widehat{C}\)
b) CM : AO là tia phân giác của\(\widehat{BAC}\)
c) CM: A,O,M thẳng hàng
d) CM : AO\(\perp\)BC
e) AM là đường trung trực của BC
2) Cho \(\widehat{PQR}\)có \(\widehat{Q}>\widehat{R}\). Vẽ tia phân giác PM ( M\(\in QR\))
a) CM : \(\widehat{PMR}-\widehat{PMQ}=\widehat{PQR}-\widehat{R}\)
b) Đường thẳng chứa tia phân giác góc ngoài tại đỉnh P của \(\Delta PQR\)cắt đường thẳng QR tại N. Cm \(2\widehat{PNQ}=\widehat{PQR}-\widehat{R}\)
1)cho tam giác ABC vuông cân tại A. M là trung điểm của BC. G thuộc AB sao cgo AGfrac{1}{3}AB, E là chân đường vuông góc hạ từ M xuống CG. MG và AC cắt nhau tại D. so sánh DE và BC2) cho tam giác ABC vuông tại A và widehat{BAC} 60 , M thuộc BC sao cho AB+BMAC+CM. tínhwidehat{CAM}3) cho tam giác ABC cân tại A , gọi E là điểm bất kì nằm giữa B và C , đường thẳng qua E vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. gọi K là trung điểm của BE. tính widehat{AKD}4)cho tam giác...
Đọc tiếp
1)cho tam giác ABC vuông cân tại A. M là trung điểm của BC. G thuộc AB sao cgo AG=\(\frac{1}{3}\)AB, E là chân đường vuông góc hạ từ M xuống CG. MG và AC cắt nhau tại D. so sánh DE và BC
2) cho tam giác ABC vuông tại A và \(\widehat{BAC}\)= 60' , M thuộc BC sao cho AB+BM=AC+CM. tính\(\widehat{CAM}\)
3) cho tam giác ABC cân tại A , gọi E là điểm bất kì nằm giữa B và C , đường thẳng qua E vuông góc với AB và đường thẳng qua C vuông góc với AC cắt nhau tại D. gọi K là trung điểm của BE. tính \(\widehat{AKD}\)
4)cho tam giác ABC cân tại A. trên đường thẳng AC lấy điểm M tùy ý.đường thẳng vuông góc với BC qua M cắt BC tại H. gọi I là trung điểm của BM. tính\(\widehat{HAI}\)
Cho tam giác ABC có \(\widehat B > \widehat C\). Tia phân giác góc BAC cắt cạnh BC tại điểm D.
a) Chứng minh \(\widehat {ADB} < \widehat {ADC}\).
b) Kẻ tia Dx nằm trong góc ADC sao cho \(\widehat {ADx} = \widehat {ADB}\). Giả sử tia Dx cắt cạnh AC tại điểm E. Chứng minh: \(\Delta ABD = \Delta AED,AB < AC\).
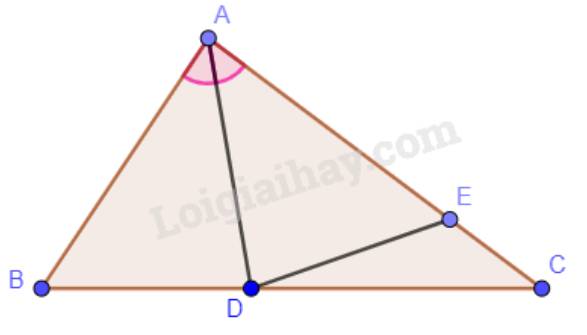
a) Ta có: \(\widehat {BAD} = \widehat {CAD}\)(vì AD là phân giác của góc BAC).
Mà \(\widehat B > \widehat C\)nên \(\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\).
Tổng ba góc trong một tam giác bằng 180° nên:
\(\begin{array}{l}\widehat B + \widehat {BAD} > \widehat C + \widehat {CAD}\\ \to 180^\circ - (\widehat B + \widehat {BAD}) < 180^\circ - (\widehat C + \widehat {CAD})\\ \to \widehat {ADB} < \widehat {ADC}\end{array}\)
b) Xét hai tam giác ADB và tam giác ADE có:
\(\widehat {ADB} = \widehat {ADE}\);
AD chung;
\(\widehat {BAD} = \widehat {EAD}\).
Vậy \(\Delta ABD = \Delta AED\) (g.c.g)
Trong một tam giác, cạnh đối diện với góc lớn hơn thì lớn hơn.
Trong tam giác ABC có \(\widehat B > \widehat C\) nên AC > AB hay AB < AC (AB là cạnh đối diện với góc C, AC là cạnh đối diện với góc B).
Đúng 0
Bình luận (0)















