a, Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu lên cạnh huyền và cạnh huyền trong tam giác vuông HBA và HCA

b, Tương tự a) và áp dụng hệ thức giữa đường cao và hình chiếu cạnh góc vuông lên cạnh huyền trong tam giác vuông ABC

a: \(\dfrac{EB}{FC}=\dfrac{BH^2}{BA}:\dfrac{CH^2}{CA}\)

\(=\dfrac{BH^2}{AB}\cdot\dfrac{AC}{CH^2}\)

\(=\dfrac{AB^4}{AC^4}\cdot\dfrac{AC}{AB}=\dfrac{AB^3}{AC^3}\)

b: \(BC\cdot BE\cdot CF\)

\(=BC\cdot\dfrac{BH^2}{AB}\cdot\dfrac{CH^2}{AC}\)

\(=\dfrac{BC}{AH\cdot BC}\cdot AH^4=\dfrac{AH^4}{AH}=AH^3\)

dsfger

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:

\(BE\cdot BA=BH^2\)

hay \(BE=\dfrac{BH^2}{BA}\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:

\(CF\cdot CA=CH^2\)

hay \(CF=\dfrac{CH^2}{CA}\)

Ta có: \(\dfrac{BE}{CF}=\dfrac{BH^2}{AB}:\dfrac{CH^2}{CA}\)

\(=\dfrac{BH^2}{CH^2}\cdot\dfrac{AC}{AB}\)

\(=\dfrac{AB^4\cdot AC}{AC^4\cdot AC}=\dfrac{AB^3}{AC^3}\)

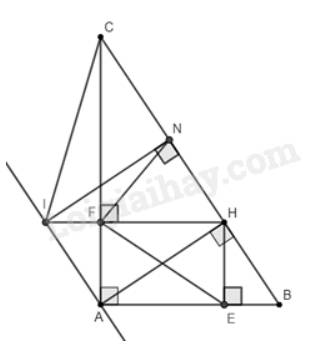
a) Vì \(AH\) là đường cao nên \(\widehat {AHB} = \widehat {AHC} = 90^\circ \)

Xét tam giác \(ABH\) và tam giác \(CBA\) có:

\(\widehat B\) (chung)

\(\widehat {AHB} = \widehat {CAB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta ABH\backsim\Delta CBA\) (g.g).

Do đó, \(\frac{{AB}}{{CB}} = \frac{{BH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{B^2} = BH.BC\) .

b)

-  Vì \(HE\) vuông góc với \(AB\) nên \(\widehat {HEA} = \widehat {HEB} = 90^\circ \)

Xét tam giác \(AHE\) và tam giác \(ABH\) có:

\(\widehat {HAE}\) (chung)

\(\widehat {HEA} = \widehat {AHB} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHE\backsim\Delta ABH\) (g.g).

Do đó, \(\frac{{AH}}{{AB}} = \frac{{AE}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AB.AE\) . (1)

- Vì \(HF\) vuông góc với \(AC\) nên \(\widehat {HFC} = \widehat {HFA} = 90^\circ \)

Xét tam giác \(AHF\) và tam giác \(ACH\) có:

\(\widehat {HAF}\) (chung)

\(\widehat {AFH} = \widehat {AHC} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta AHF\backsim\Delta ACH\) (g.g).

Do đó, \(\frac{{AH}}{{AC}} = \frac{{AF}}{{AH}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)

Suy ra, \(A{H^2} = AF.AC\) . (2)

Từ (1) và (2) suy ra, \(AE.AB = AF.AC\) (điều phải chứng minh)

c) Vì \(AE.AB = AF.AC \Rightarrow \frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\).

Xét tam giác \(AFE\) và tam giác \(ABC\) có:

\(\widehat A\) (chung)

\(\frac{{AE}}{{AC}} = \frac{{AF}}{{AB}}\) (chứng minh trên)

Suy ra, \(\Delta AFE\backsim\Delta ABC\) (c.g.c).

d) Vì \(HF\) vuông góc với \(AC\) nên \(CF \bot HI\), do đó, \(\widehat {CFH} = \widehat {CFI} = 90^\circ \).

Vì \(IN \bot CH \Rightarrow \widehat {CBI} = \widehat {HNI} = 90^\circ \).

Xét tam giác \(HFC\) và tam giác \(HNI\) có:

\(\widehat {CHI}\) (chung)

\(\widehat {HFC} = \widehat {HNI} = 90^\circ \) (chứng minh trên)

Suy ra, \(\Delta HFC\backsim\Delta HNI\) (g.g).

Suy ra, \(\frac{{HF}}{{HN}} = \frac{{HC}}{{HI}}\) (hai cặp cạnh tương ứng cùng tỉ lệ)

Do đó, \(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\).

Xét tam giác \(HNF\) và tam giác \(HIC\) có:

\(\widehat {CHI}\) (chung)

\(\frac{{HF}}{{HC}} = \frac{{HN}}{{HI}}\) (chứng minh trên)

Suy ra, \(\Delta HNF\backsim\Delta HIC\) (c.g.c).