làm hộ mk bài này với,cám ơn trước nhá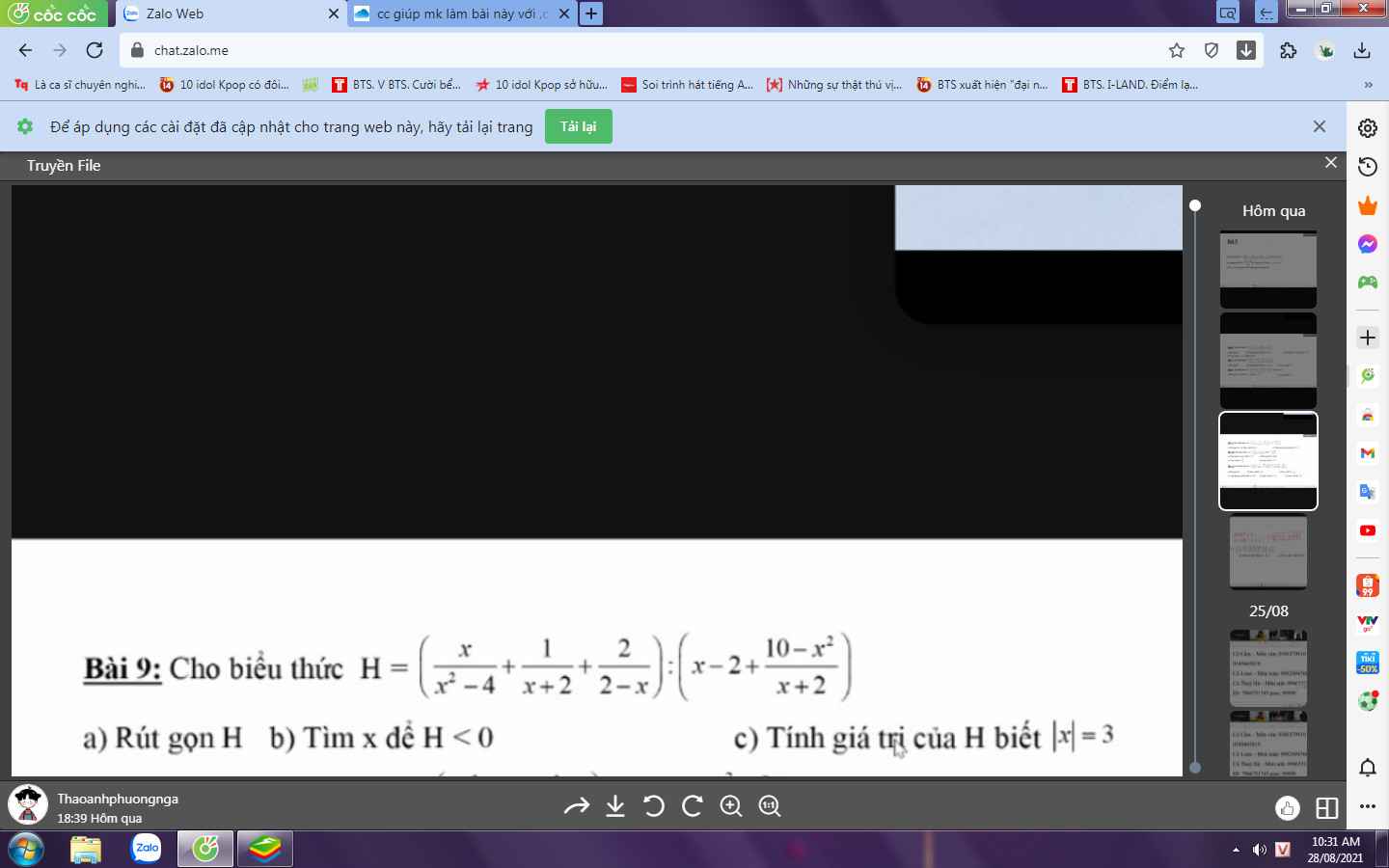

Những câu hỏi liên quan
cc giúp mk làm bài này với ,cảm ơn trước nhá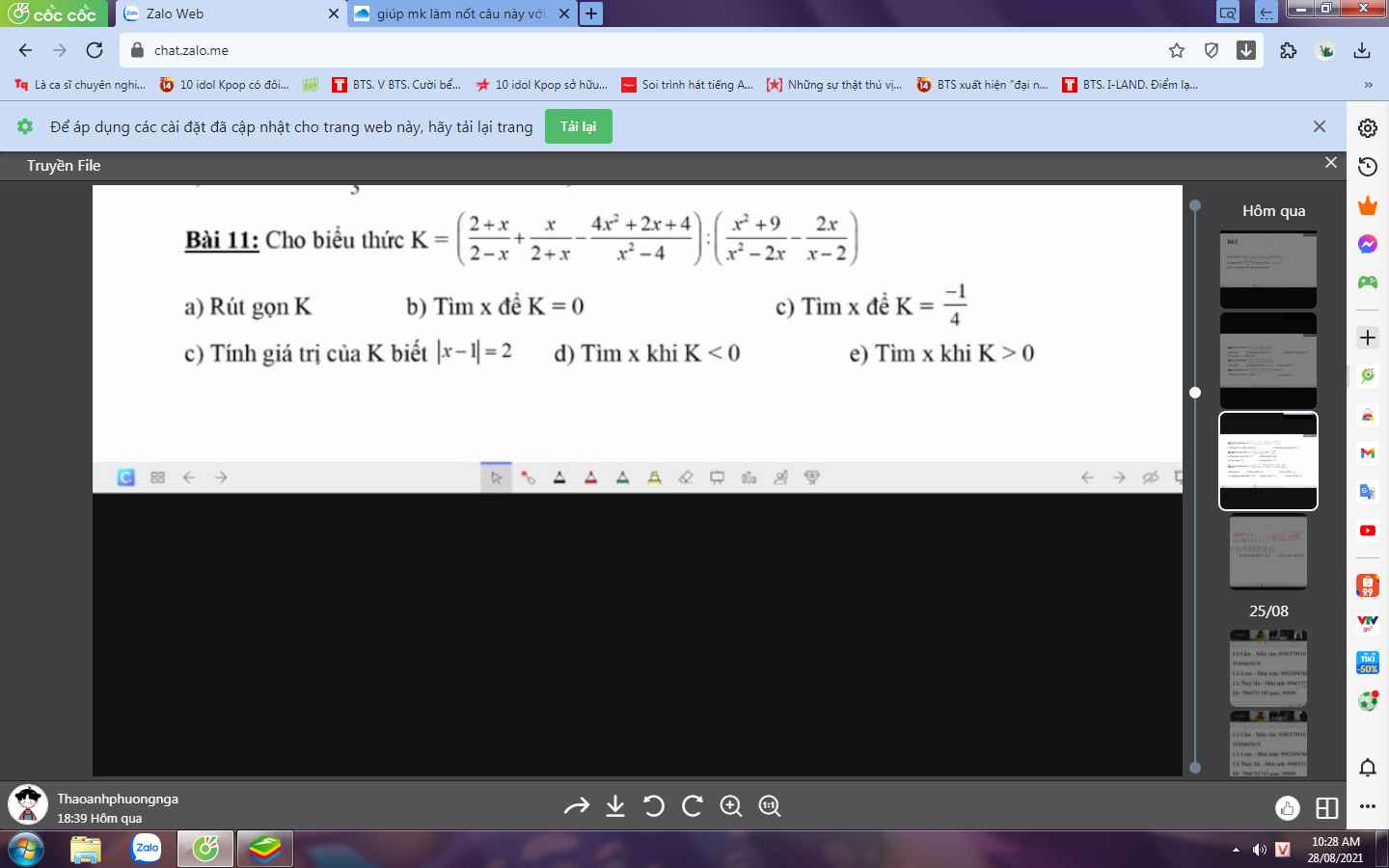
a: Ta có: \(K=\left(\dfrac{2+x}{2-x}+\dfrac{x}{2+x}-\dfrac{4x^2+2x+4}{x^2-4}\right):\left(\dfrac{x^2+9}{x^2-2x}-\dfrac{2x}{x-2}\right)\)
\(=\dfrac{-x^2-4x-4+x^2-2x-4x^2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2+9-2x^2}{x\left(x-2\right)}\)
\(=\dfrac{-4x^2-8x-8}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x\left(x-2\right)}{-x^2+9}\)
\(=\dfrac{-4\left(x^2+2x+1\right)}{x+2}\cdot\dfrac{x}{-\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{-4x\left(x+1\right)^2}{-\left(x-3\right)\left(x+3\right)\left(x+2\right)}\)
Đúng 0
Bình luận (0)
Câu 5 làm hộ mk nhá cần gấp mai thi nhoa cám ơn các bạn :))
\(=>5.4200\left(t2-35\right)=315000=>t2=50^OC\)
Đúng 2
Bình luận (0)
giúp mk làm nốt câu này với,cảm ơn trước nhá
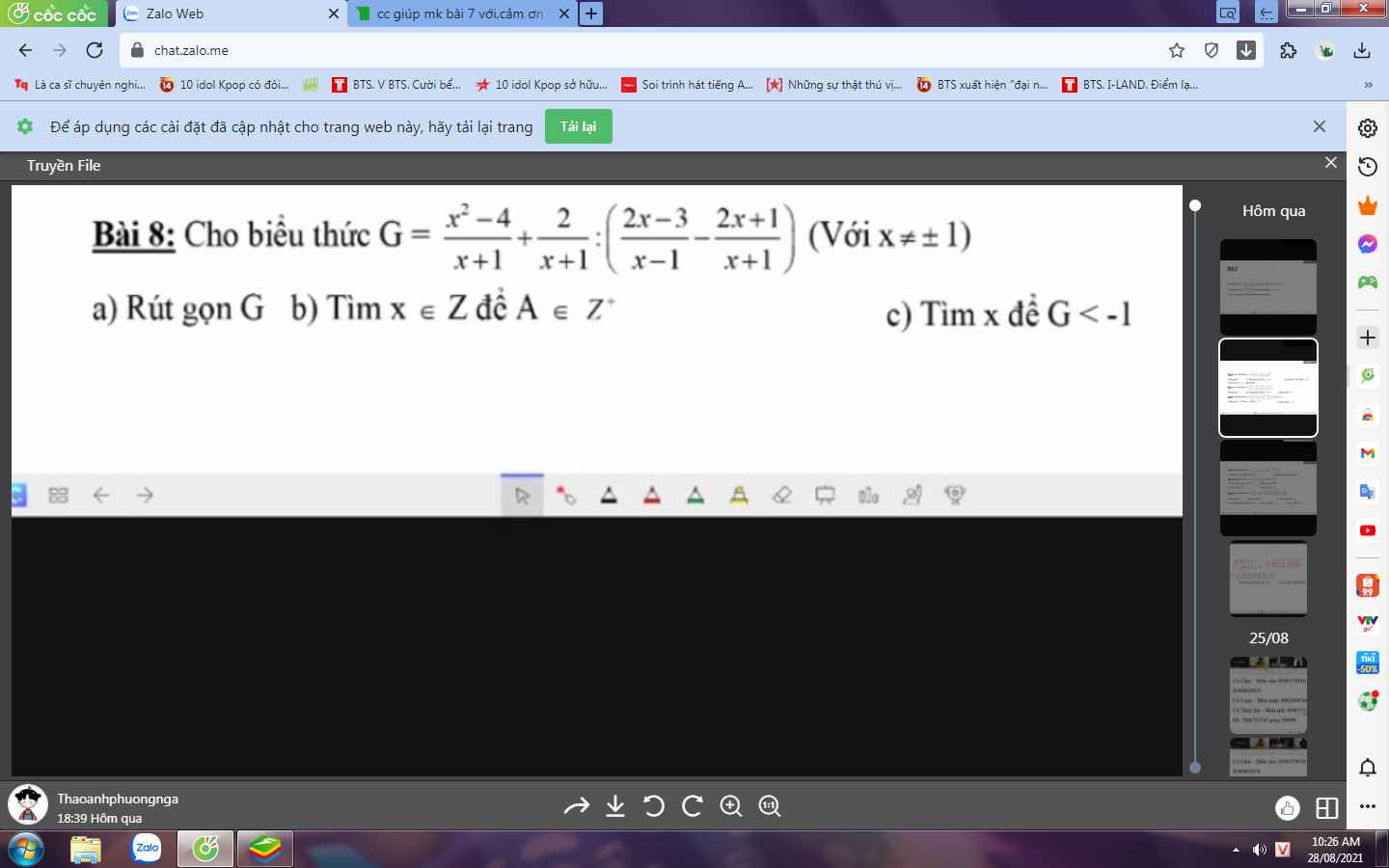
Lời giải:
a.
\(G=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{(2x-3)(x+1)-(2x+1)(x-1)}{(x-1)(x+1)}\)
\(=\frac{x^2-4}{x+1}+\frac{2}{x+1}:\frac{-2}{(x-1)(x+1)}=\frac{x^2-4}{x+1}+\frac{2}{x+1}.\frac{(x+1)(x-1)}{-2}\)
\(=\frac{x^2-4}{x+1}-(x-1)=\frac{x^2-4-(x^2-1)}{x+1}=\frac{-3}{x+1}\)
b.
Để $A\in\mathbb{Z}^+$ thì $x+1$ là ước âm của $-3$
$\Rightarrow x+1\in\left\{-1;-3\right\}$
$\Leftrightarrow x\in\left\{-2;-4\right\}$ (tm)
c.
$G< -1\Leftrightarrow \frac{-3}{x+1}+1< 0$
$\Leftrightarrow \frac{x-2}{x+1}< 0$
$\Leftrightarrow x-2<0< x+1$ hoặc $x-2>0>x+1$
$\Leftrightarrow -1< x< 2$ (chọn) hoặc $-1> x>2$ (loại)
Vậy $-1< x< 2$ và $x\neq 1$
Đúng 1
Bình luận (1)
Bài 8:
a: Ta có: \(G=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\left(\dfrac{2x-3}{x-1}-\dfrac{2x+1}{x+1}\right)\)
\(=\dfrac{x^2-4}{x+1}+\dfrac{2}{x+1}:\dfrac{2x^2+2x-3x-3-2x^2+2x-x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{2}{x+1}\cdot\dfrac{\left(x-1\right)\left(x+1\right)}{-2}\)
\(=\dfrac{\left(x-2\right)\left(x+2\right)}{x+1}+\dfrac{-x+1}{1}\)
\(=\dfrac{x^2-4-\left(x-1\right)\left(x+1\right)}{x+1}\)
\(=\dfrac{x^2-4-x^2+1}{x+1}\)
\(=-\dfrac{3}{x+1}\)
Đúng 1
Bình luận (1)
c: Để G<-1 thì G+1<0
\(\Leftrightarrow\dfrac{-3+x+1}{x+1}< 0\)
\(\Leftrightarrow\dfrac{x-2}{x+1}< 0\)
\(\Leftrightarrow-1< x\le2\)
Kết hợp ĐKXĐ, ta được:
\(\left\{{}\begin{matrix}-1< x\le2\\x\ne1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
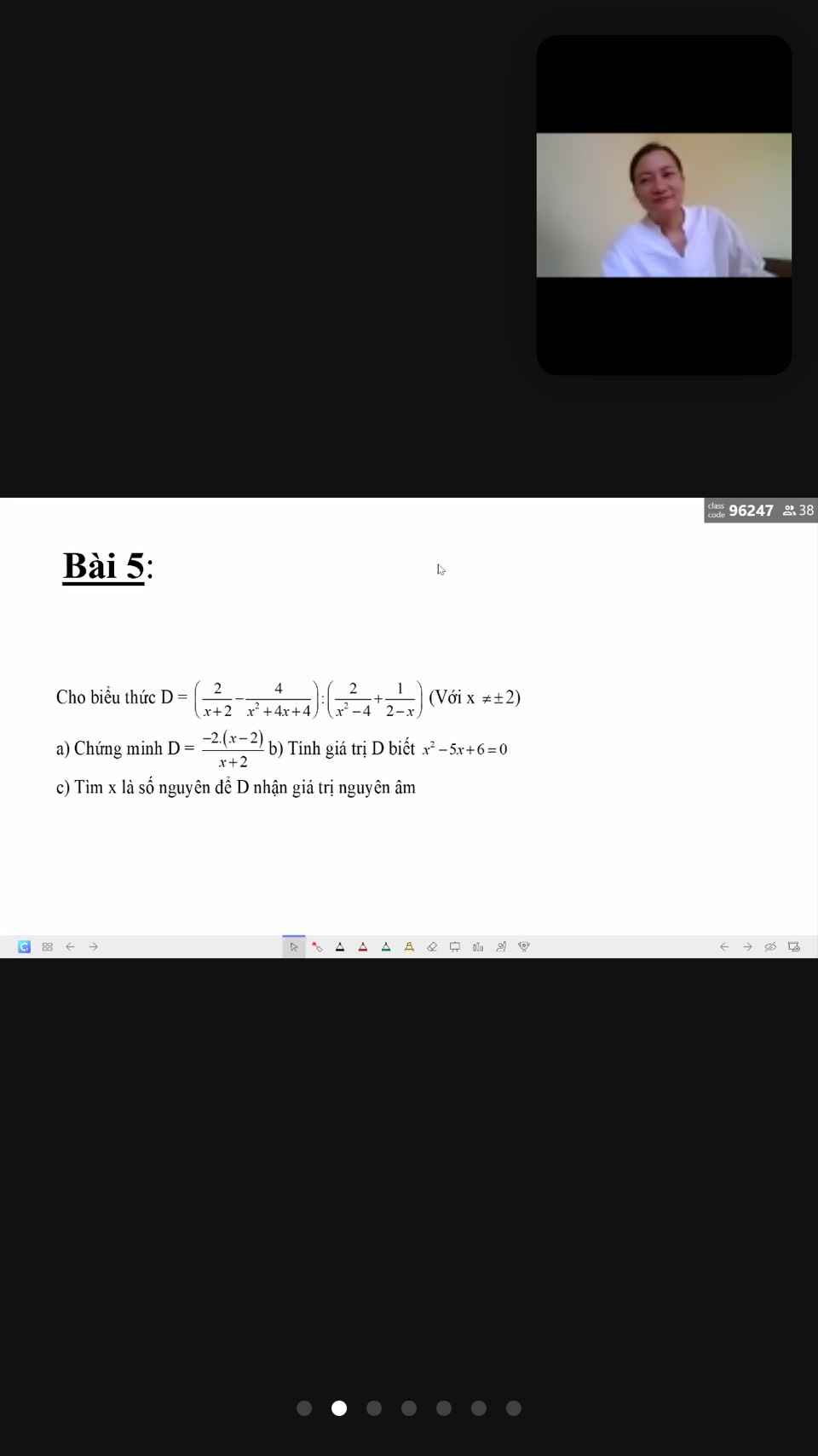 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
a) \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)\(=\left(\dfrac{2}{x+2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x-2}\right)\)
\(=\left(\dfrac{2\left(x+2\right)}{\left(x+2\right)^2}-\dfrac{4}{\left(x+2\right)^2}\right):\left(\dfrac{2}{\left(x-2\right)\left(x+2\right)}-\dfrac{x+2}{\left(x-2\right)\left(x+2\right)}\right)\)
\(=\dfrac{2\left(x+2\right)-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{-x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}.\dfrac{\left(x-2\right)\left(x+2\right)}{-x}\)
\(=\dfrac{-2.\left(x-2\right)}{x+2}\)
\(x^2-5x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
\(P=\dfrac{-2.\left(x-2\right)}{x+2}\)
Thay \(x=2\), ta có:
\(P=\dfrac{-2.\left(2-2\right)}{2+2}\)
\(=0\)
Thay \(x=3\), ta có:
\(P=\dfrac{-2.\left(3-2\right)}{3+2}\)
\(=-\dfrac{2}{5}\)
Đúng 3
Bình luận (2)
D nguyên âm \(\left[{}\begin{matrix}\left\{{}\begin{matrix}-2\left(x-2\right)< 0\\x+2>0\end{matrix}\right.\\\left\{{}\begin{matrix}-2\left(x-2\right)>0\\x+2< 0\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>2\\x>-2\end{matrix}\right.\\\left\{{}\begin{matrix}x< 2\\x< -2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x>2\\x< -2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
a:Ta có: \(D=\left(\dfrac{2}{x+2}-\dfrac{4}{x^2+4x+4}\right):\left(\dfrac{2}{x^2-4}+\dfrac{1}{2-x}\right)\)
\(=\dfrac{2x+4-4}{\left(x+2\right)^2}:\dfrac{2-x-2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{2x}{\left(x+2\right)^2}\cdot\dfrac{\left(x+2\right)\left(x-2\right)}{-x}\)
\(=\dfrac{-\left(x-2\right)}{x+2}\)
b: Ta có: \(x^2-5x+6=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
hay x=3
Thay x=3 vào D, ta được:
\(D=\dfrac{-\left(3-2\right)}{3+2}=-\dfrac{1}{5}\)
Đúng 1
Bình luận (1)
mn ơi lm giúp mk câu này với mk cám ơn trước
Đọc tiếp
mn ơi lm giúp mk câu này với mk cám ơn trước
Giúp mình làm 2 bài này với mọi người cám ơn trước nhaa 
bài 26: gọi quãng đường đi là S
=|> thời gian đi với v1: t1=S/12
thòi gia đi quãng đường với v2 là :t2=S/15
theo đề ta có pt: t1=t2+1
<=>\(\frac{S}{12}=\frac{S}{15}+1\)
<=> \(\frac{S}{60}=1\)
=> S=60km
Đúng 0
Bình luận (1)
làm hộ mình bài này với
mk cảm ơn trước nha

làm hộ mk với mai mk phải nộp rồi,cảm ơn truovcs nhá
Bài 10:
a: Thay x=3 vào A, ta được:
\(A=\left(\dfrac{1}{3+2}+\dfrac{1}{3^2-4}\right)=\dfrac{1}{5}+\dfrac{1}{5}=\dfrac{2}{5}\)
b: Ta có: P=AB
\(=\left(\dfrac{1}{x+2}+\dfrac{1}{x^2-4}\right)\cdot\dfrac{x^2+2x}{x-1}\)
\(=\dfrac{x-2+1}{\left(x+2\right)\left(x-2\right)}\cdot\dfrac{x\left(x+2\right)}{x-1}\)
\(=\dfrac{x-1}{x-2}\cdot\dfrac{x}{x-1}\)
\(=\dfrac{x}{x-2}\)
c: Để \(P=\dfrac{2}{3}\) thì \(\dfrac{x}{x-2}=\dfrac{2}{3}\)
\(\Leftrightarrow3x=2x-4\)
hay x=-4(nhận)
Đúng 0
Bình luận (0)
Làm hộ mình bài cuối với!! Cám ơn các bạn!!!
Đặt \(\left\{{}\begin{matrix}b+c-a=x\\c+a-b=y\\a+b-c=z\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+y=2c\\y+z=2a\\z+x=2b\end{matrix}\right.\)
\(\Leftrightarrow P=\dfrac{2\left(y+z\right)}{x}+\dfrac{9\left(x+z\right)}{2y}+\dfrac{8\left(x+y\right)}{z}\\ \Leftrightarrow P=\dfrac{2y}{x}+\dfrac{2z}{x}+\dfrac{9x}{2y}+\dfrac{9z}{2y}+\dfrac{8x}{z}+\dfrac{8y}{z}\\ \Leftrightarrow P=\left(\dfrac{2y}{x}+\dfrac{9x}{2y}\right)+\left(\dfrac{2z}{x}+\dfrac{8x}{z}\right)+\left(\dfrac{9z}{2y}+\dfrac{8y}{z}\right)\\ \Leftrightarrow P\ge2\sqrt{\dfrac{18xy}{2xy}}+2\sqrt{\dfrac{16xz}{xz}}+2\sqrt{\dfrac{72yz}{2yz}}\\ \Leftrightarrow P\ge2\sqrt{9}+2\sqrt{16}+2\sqrt{36}=26\)
Đúng 1
Bình luận (3)















