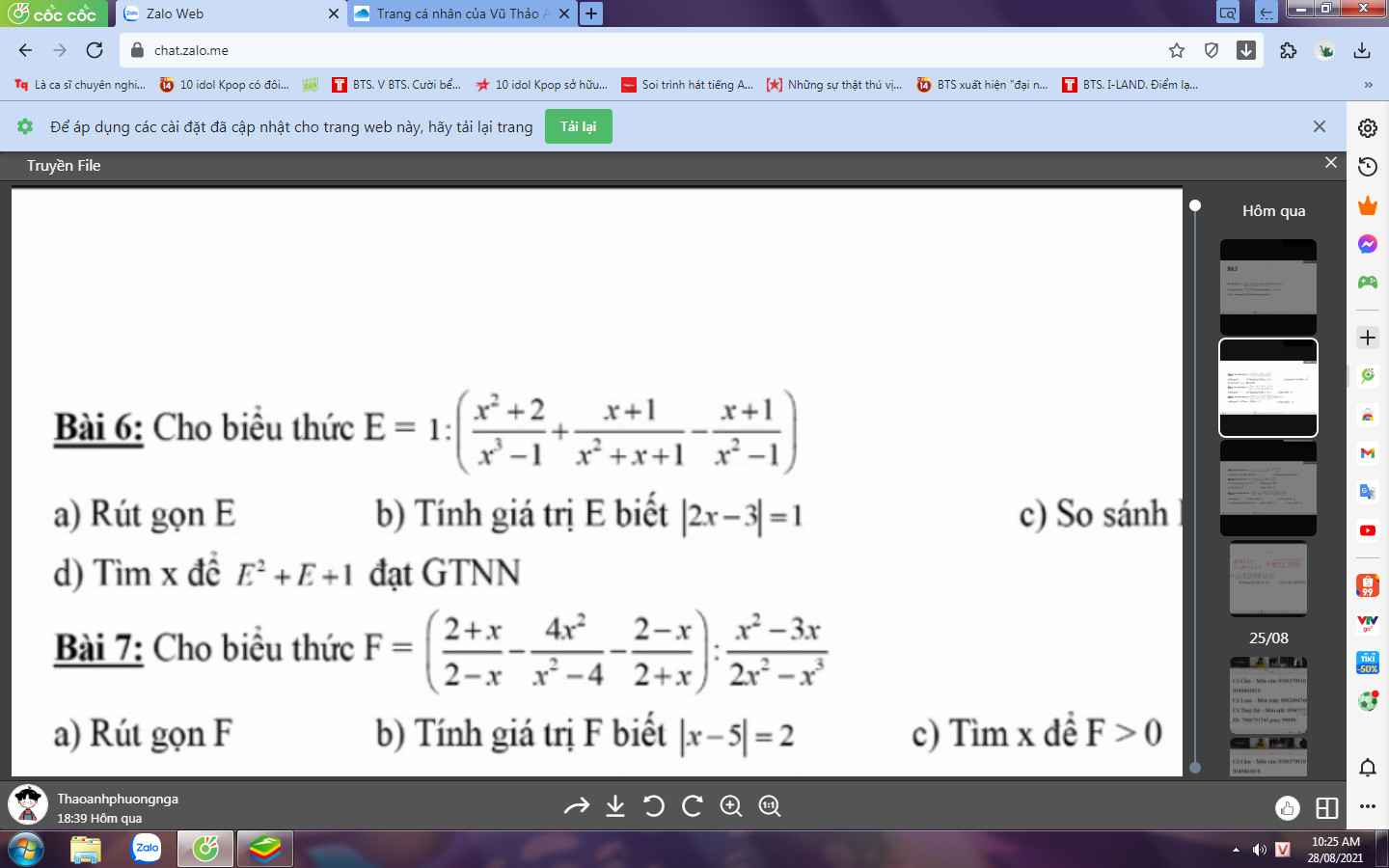
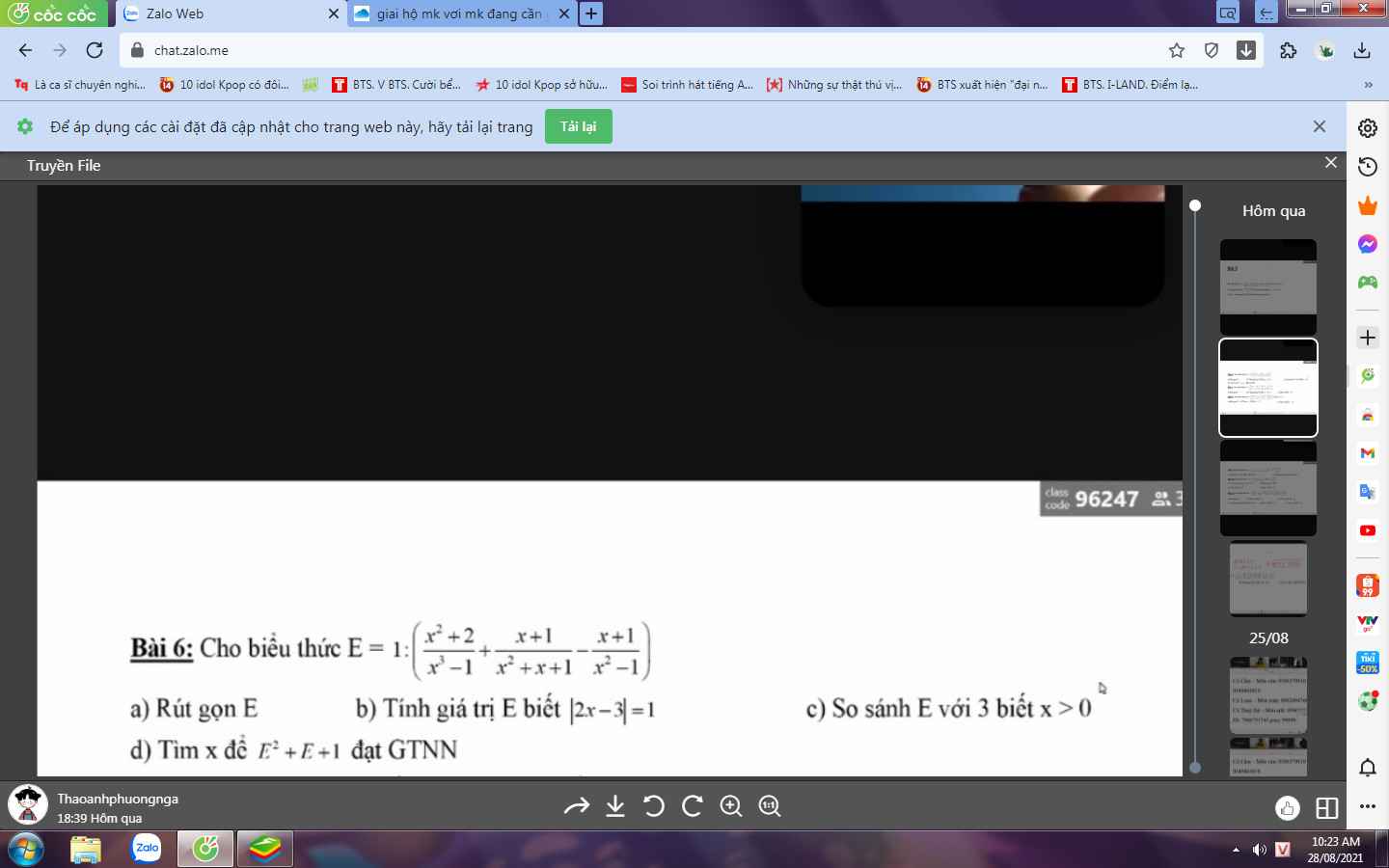
a) Ta có:
\(H=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}+\dfrac{2}{2-x}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\\ =\left(\dfrac{x}{x^2-4}+\dfrac{x-2}{x^2-4}-\dfrac{2\left(x+2\right)}{x^2-4}\right):\left(\dfrac{x^2-4+10-x^2}{x+2}\right)\\ =\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}\\ =\dfrac{-6}{x-2}\cdot\dfrac{1}{6}=\dfrac{1}{2-x}\)
b) Để H < 0 thì \(\dfrac{1}{2-x}\) < 0 hay 2 - x < 0 ( do 1 > 0) suy ra x > 2
Vậy với x > 2 thì H < 0.
c) Ta có:
\(\left|x\right|=3\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
+) Với x = 3 thì:
H = \(\dfrac{1}{2-3}=-1\)
+) Với x = -3 thì:
\(H=\dfrac{1}{2-\left(-3\right)}=\dfrac{1}{5}\)
Vậy với |x| = 3 thì H = -1 hoặc H = 1/5
a: Ta có: \(H=\left(\dfrac{x}{x^2-4}+\dfrac{1}{x+2}+\dfrac{2}{2-x}\right):\left(x-2+\dfrac{10-x^2}{x+2}\right)\)
\(=\dfrac{x+x-2-2x-4}{\left(x-2\right)\left(x+2\right)}:\dfrac{x^2-4+10-x^2}{x+2}\)
\(=\dfrac{-6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x+2}{6}\)
\(=\dfrac{-1}{x-2}\)
b: Để H<0 thì x-2<0
hay x<2
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x< 2\\x\ne-2\end{matrix}\right.\)
c: Ta có: |x|=3
nên \(\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\)
Thay x=3 vào H, ta được:
\(H=\dfrac{-1}{3-2}=-1\)
Thay x=-3 vào H, ta được:
\(H=\dfrac{-1}{-3-2}=\dfrac{-1}{-5}=\dfrac{1}{5}\)

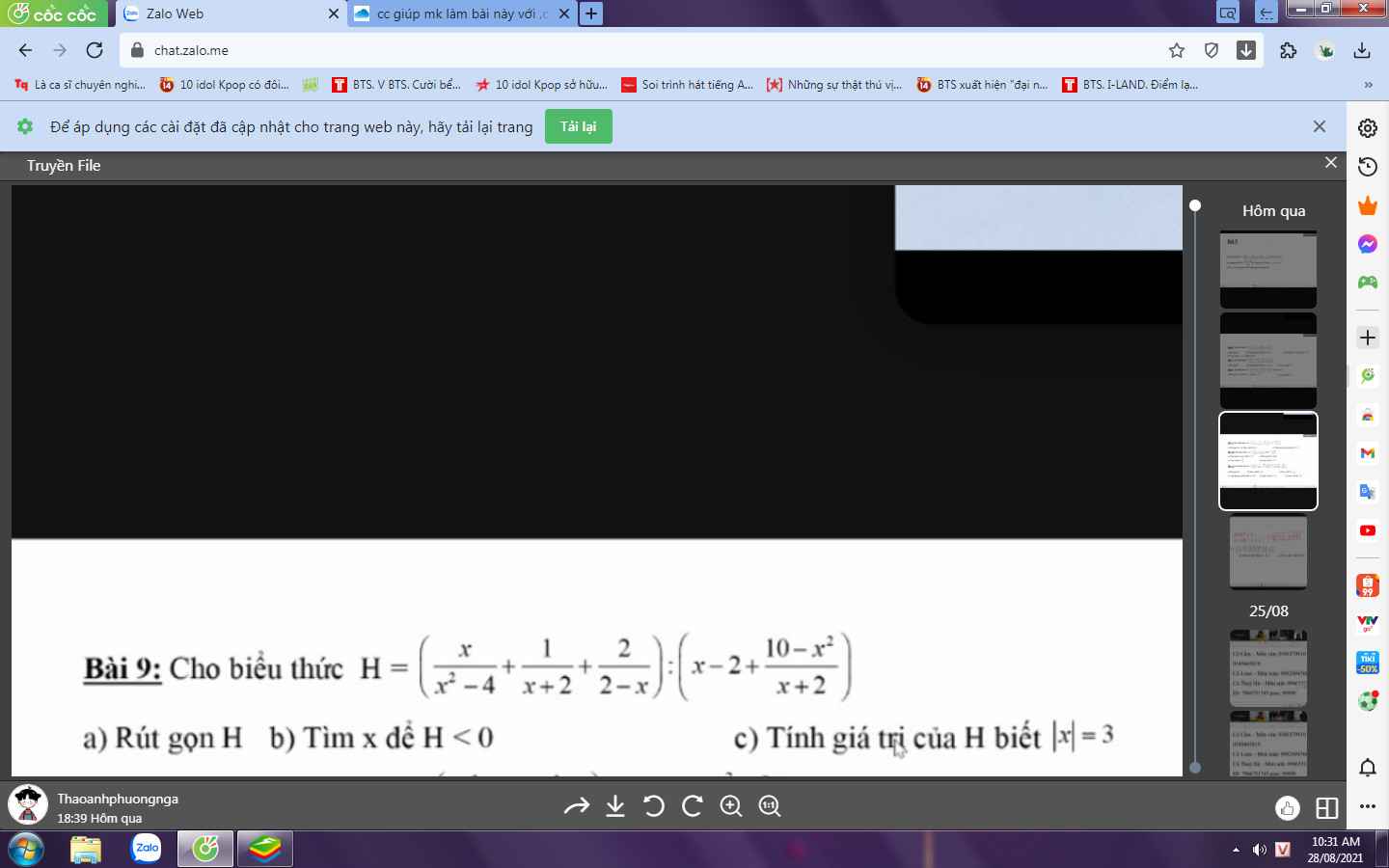





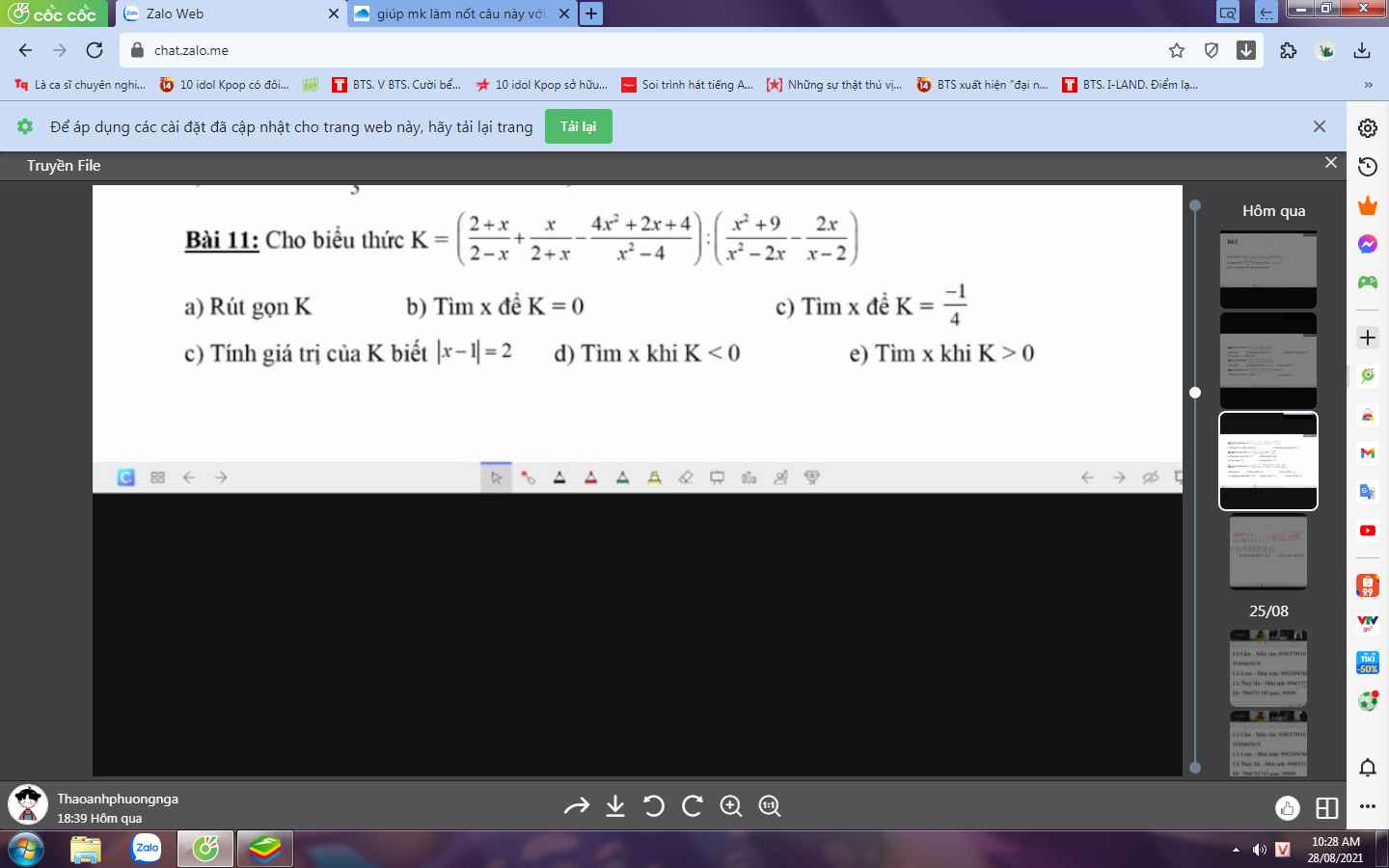
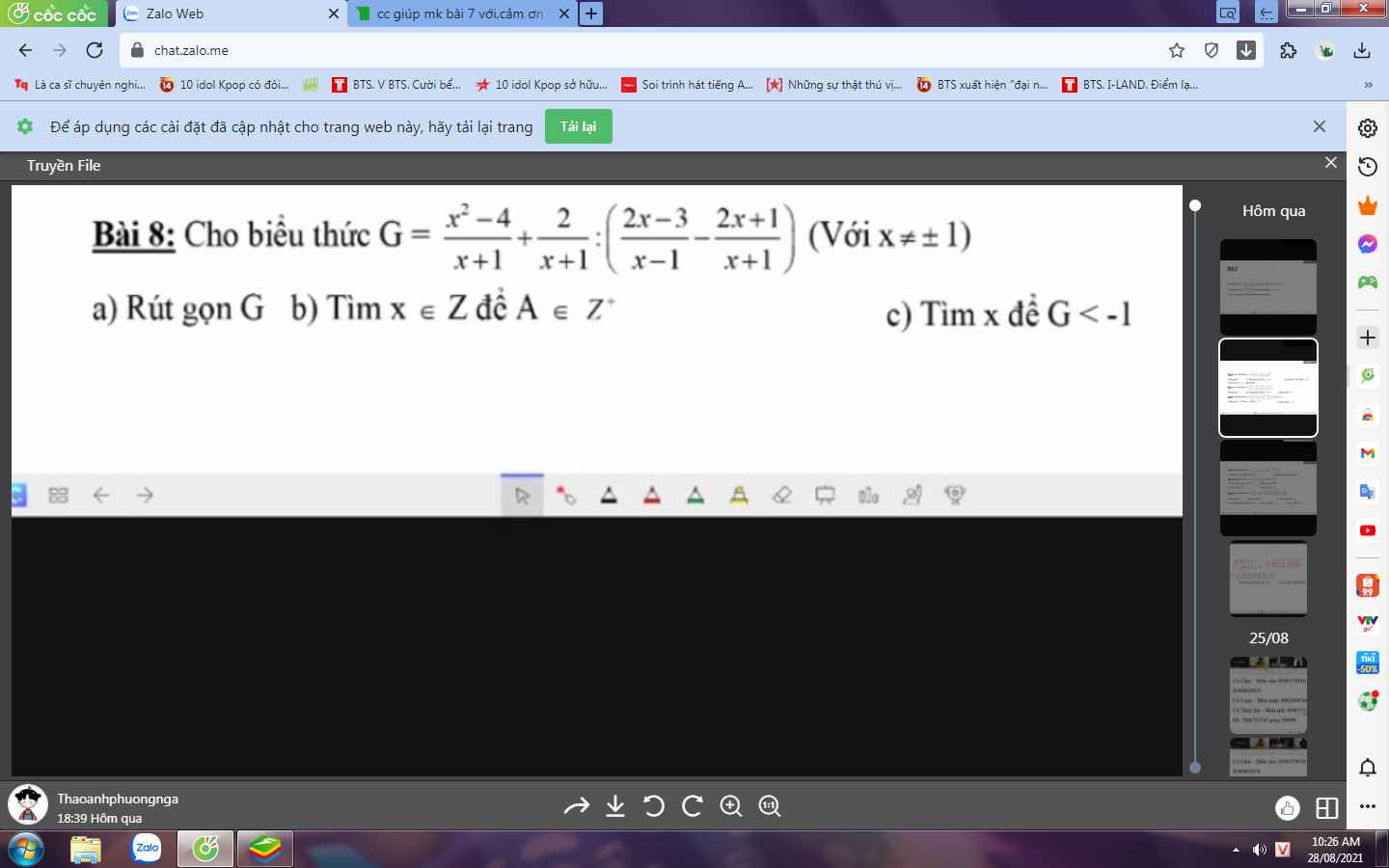
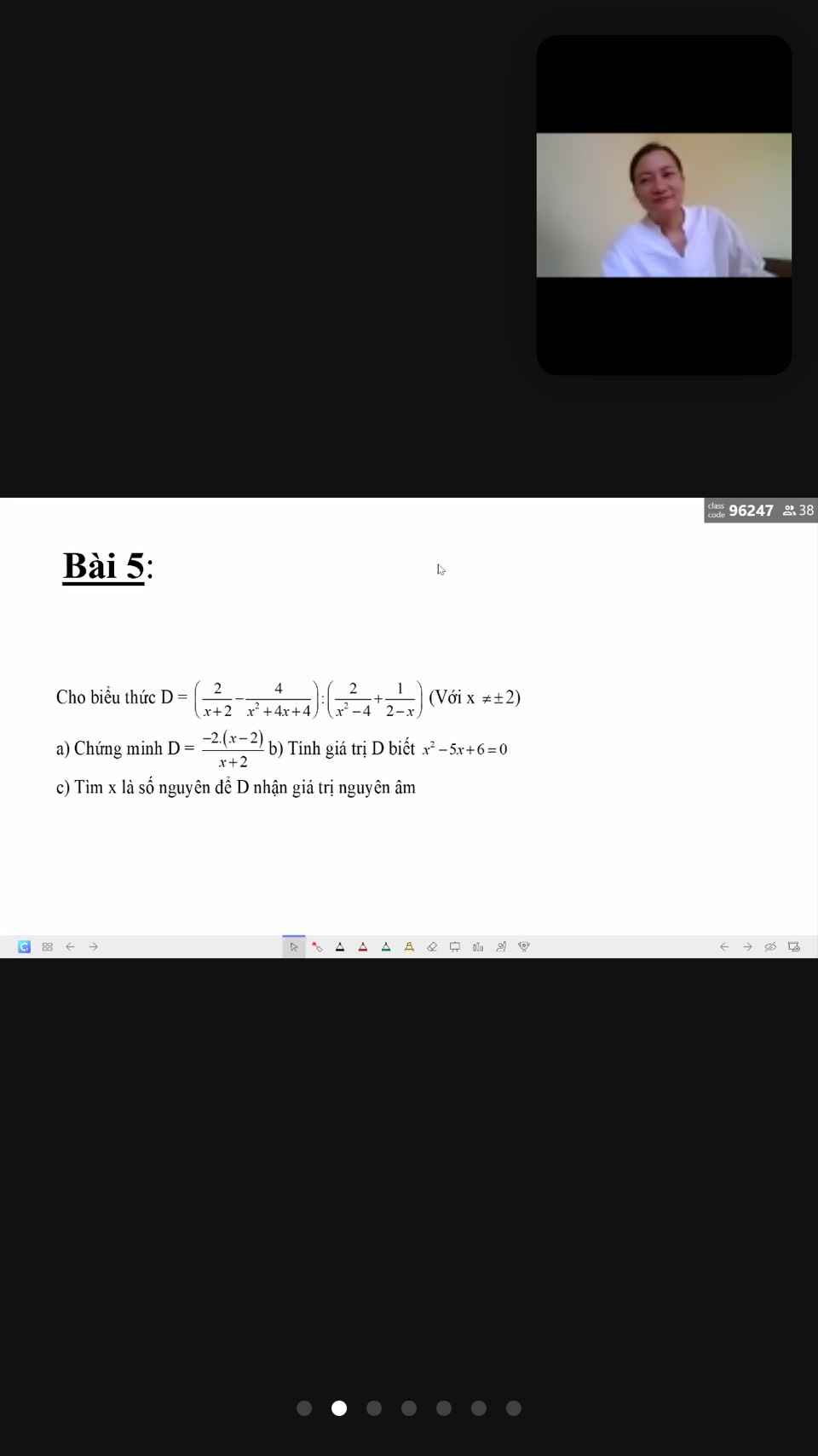 giúp mk làm nốt mấy câu này với,cảm ơn trước nhá
giúp mk làm nốt mấy câu này với,cảm ơn trước nhá