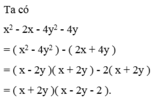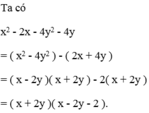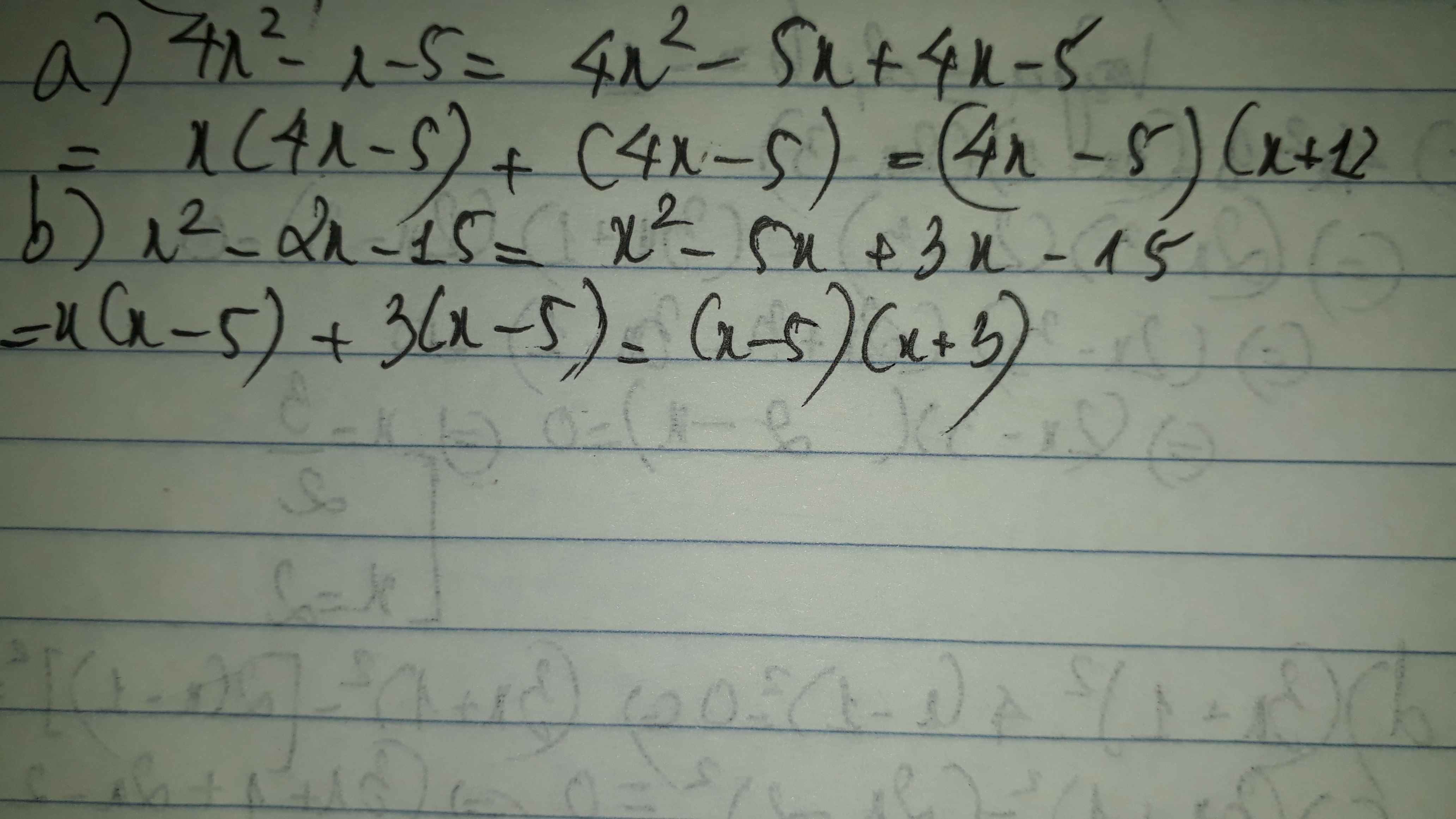phân tích đa thức sau thành nhân tử bằng phương pháp nhóm hạng tử :
x2 - 2x - 4y2 - 4y

Những câu hỏi liên quan
PHÂN TÍCH CÁC ĐA THỨC SAU THÀNH NHÂN TỬ BẰNG PHƯƠNG PHÁP NHÓM NHIỀU HẠNG TỬ :
a) x2 -2x -4y2-4y
b) x4 + 2x3 - 4x -4
c) x3 + 2x2y -x -2y
d) 3x2 -3y2 -2(x-y)2
e) x3 -4x2 -9x +36
f) x2 -y2 -2x -2y
a: Ta có: \(x^2-4y^2-2x-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
c: Ta có: \(x^3+2x^2y-x-2y\)
\(=x^2\left(x+2y\right)-\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
d: Ta có: \(3x^2-3y^2-2\cdot\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\cdot\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
Đúng 2
Bình luận (0)
e: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
f: Ta có: \(x^2-y^2-2x-2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-2\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
x2-4y2-2x+1
x+2a(x-y)-y
\(x^2-4y^2-2x+1=\left(x-1\right)^2-4y^2=\left(x-1-2y\right)\left(x-1+2y\right)\)
Đúng 1
Bình luận (0)
phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử:
a) x2 ( x+ 2y) -x -2y
b)3x2- 3y2 -2 (x-y)2
c) x^2- 2x-4y2 - 4y
d) x3 - 4x2 - 9x +36
các bạn giải giúp mình với. Mình đang cần gấp
a) x2 ( x+ 2y) -x -2y
= x2 ( x+ 2y) -(x+2y)
= (x2-1)(x+2y)
= (x-1)(x+1)(x+2y)
b)3x2- 3y2 -2 (x-y)2
= 3(x2-y2) -2 (x-y)2
= 3(x-y)(x+y)-2(x-y)(x-y)
\(=\left(x-y\right)\left[3\left(x+y\right)-2\left(x-y\right)\right]\\ =\left(x-y\right)\left(3x+3y-2x+2y\right)\\ =\left(x-y\right)\left(x+5y\right)\)
c) x2- 2x-4y2 - 4y
= (x2-4y2)-(2x+4y)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\\ =\left(x+2y\right)\left(x-2y-2\right)\)
d) x3 - 4x2 - 9x +36
= (x3+3x2)-(7x2+21x)+(12x+36)
= x2(x+3)-7x(x+3)+12(x+3)
=(x2-7x+12)(x+3)
\(=\left[\left(x^2-3x\right)-\left(4x-12\right)\right]\left(x+3\right)\\ =\left[x\left(x-3\right)-4\left(x-3\right)\right]\left(x+3\right)=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
Đúng 2
Bình luận (1)
a) = x2 ( x+ 2y) -(x+2y)
= (x2-1)(x+2y)
= (x-1)(x+1)(x+2y)
b)= 3(x2-y2) -2 (x-y)2
= 3(x-y)(x+y)-2(x-y)(x-y)
=(x−y)[3(x+y)−2(x−y)]
=(x−y)(3x+3y−2x+2y)
=(x−y)(x+5y)
=(x−y)[3(x+y)−2(x−y)]
=(x−y)(3x+3y−2x+2y)
=(x−y)(x+5y)
c)= (x2-4y2)-(2x+4y)
=(x−2y)(x+2y)−2(x+2y)
=(x+2y)(x−2y−2)
=(x−2y)(x+2y)−2(x+2y)
=(x+2y)(x−2y−2)
d)= (x3+3x2)-(7x2+21x)+(12x+36)
= x2(x+3)-7x(x+3)+12(x+3)
=(x2-7x+12)(x+3)
=[(x2−3x)−(4x−12)](x+3)
=[x(x−3)−4(x−3)](x+3)
=(x−4)(x−3)(x+3)
Đúng 1
Bình luận (1)
a: \(x^2\left(x+2y\right)-x-2y\)
\(=\left(x+2y\right)\left(x^2-1\right)\)
\(=\left(x+2y\right)\left(x-1\right)\left(x+1\right)\)
b: \(3x^2-3y^2-2\left(x-y\right)^2\)
\(=3\left(x-y\right)\left(x+y\right)-2\left(x-y\right)^2\)
\(=\left(x-y\right)\left(3x+3y-2x+2y\right)\)
\(=\left(x-y\right)\left(x+5y\right)\)
c: Ta có: \(x^2-2x-4y^2-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
d: Ta có: \(x^3-4x^2-9x+36\)
\(=x^2\left(x-4\right)-9\left(x-4\right)\)
\(=\left(x-4\right)\left(x^2-9\right)\)
\(=\left(x-4\right)\left(x-3\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử (bằng phương pháp nhóm hạng tử)
c/ 5x2 + 3y + 15x + xy d/ x2 + 6x + 9 – y2
e/ x2 – y2 + 2x + 1 f/ x2 – 2xy – 9 + y2
c) \(5x^2+3y+15x+xy=5x\left(x+3\right)+y\left(x+3\right)=\left(x+3\right)\left(5x+y\right)\)
d) \(x^2+6x+9-y^2=\left(x+3\right)^2-y^2=\left(x+3-y\right)\left(x+3+y\right)\)
e) \(x^2-y^2+2x+1=\left(x^2+2x+1\right)-y^2=\left(x+1\right)^2-y^2=\left(x+1-y\right)\left(x+1+y\right)\)
f) \(x^2-2xy-9+y^2=\left(x^2-2xy+y^2\right)-9=\left(x-y\right)^2-3^2=\left(x-y-3\right)\left(x-y+3\right)\)
Đúng 1
Bình luận (0)
c: \(5x^2+15x+3y+xy\)
\(=5x\left(x+3\right)+y\left(x+3\right)\)
\(=\left(x+3\right)\left(5x+y\right)\)
d: \(x^2+6x+9-y^2\)
\(=\left(x+3\right)^2-y^2\)
\(=\left(x+3-y\right)\left(x+3+y\right)\)
e: \(x^2+2x+1-y^2\)
\(=\left(x+1\right)^2-y^2\)
\(=\left(x+1-y\right)\left(x+1+y\right)\)
f: \(x^2-2xy+y^2-9\)
\(=\left(x-y\right)^2-9\)
\(=\left(x-y-3\right)\left(x-y+3\right)\)
Đúng 1
Bình luận (0)
Phân tích các đa thức sau thành nhân tử x 2 - 2 x - 4 y 2 - 4 y
Phân tích các đa thức sau thành nhân tử x 2 - 2 x - 4 y 2 - 4 y
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung:
-x2-4xy-4y2
= \(-\left(x^2+4xy+4y^2\right)\)
= \(-\left(x+2y\right)^2\)
Đúng 1
Bình luận (0)
Phân tích đa thức thành nhân tử x2-2x-4y2-4y
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)=\left(x+2y\right)\left(x-2y-2\right)\)
Đúng 1
Bình luận (0)
= ( x2 - 4y2 ) - ( 2x + 4y )
= ( x - 2y ) ( x + 2y ) - 2 ( x - 2y )
= ( x - 2y ) ( x + 2y - 2 )
Đúng 1
Bình luận (0)
Phân tích đa thức sau thành nhân tử bằng phương pháp nhóm nhiều hạng tử :
a) ( x - 3)( x - 1) - 3(x-3)
b) x³ - 2x² + 2x - 13
c) x²y + xy + x + 1
d) x² - ( a+b)x + ab
e) x² - 2x -4y² - 4y
a) \(\left(x-3\right)\left(x-1\right)-3\left(x-3\right)\)
\(=\left(x-3\right)\left(x-1-3\right)\)
\(=\left(x-3\right)\left(x-4\right)\)
Đúng 0
Bình luận (0)
c) x^2y+xy+x+1=xy(x+1)+x+1=(x+1)(xy+1) d)x^2-ax-bx+ab=x(x-a)-b(x-a)=(x-a)(x-b) d) (x^2-4y^2)-(2x+4y)=(x+2y)(x-2y)-2(x+2y)=(x+2y)(x-2y-2)
Đúng 0
Bình luận (0)
a)\((x-3)(x-1)-3(x-3)\)
\(=\left(x-3\right)\left(x-4\right)\)
b)\(x^3-2x^2+2x-13\)
Sai đề
c)\(x^2y+xy+x+1\)
\(=\left(x+1\right)\left(xy+1\right)\)
d)\(x^2-(a+b)x+ab\)
\(=\left(x-a\right)\left(x-b\right)\)
e)\(x^2-2x-4y^2-4y\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1: Phân tích đa thức sau thành nhân tử ( làm bằng 2 cách: nhóm các hạng tử, tách hạng tử )
a,4x2 - x - 5
b,x2 - 2x - 15
a: \(4x^2-x-5=\left(4x-5\right)\left(x+1\right)\)
b: \(x^2-2x-15=\left(x-5\right)\left(x+3\right)\)
Đúng 0
Bình luận (0)