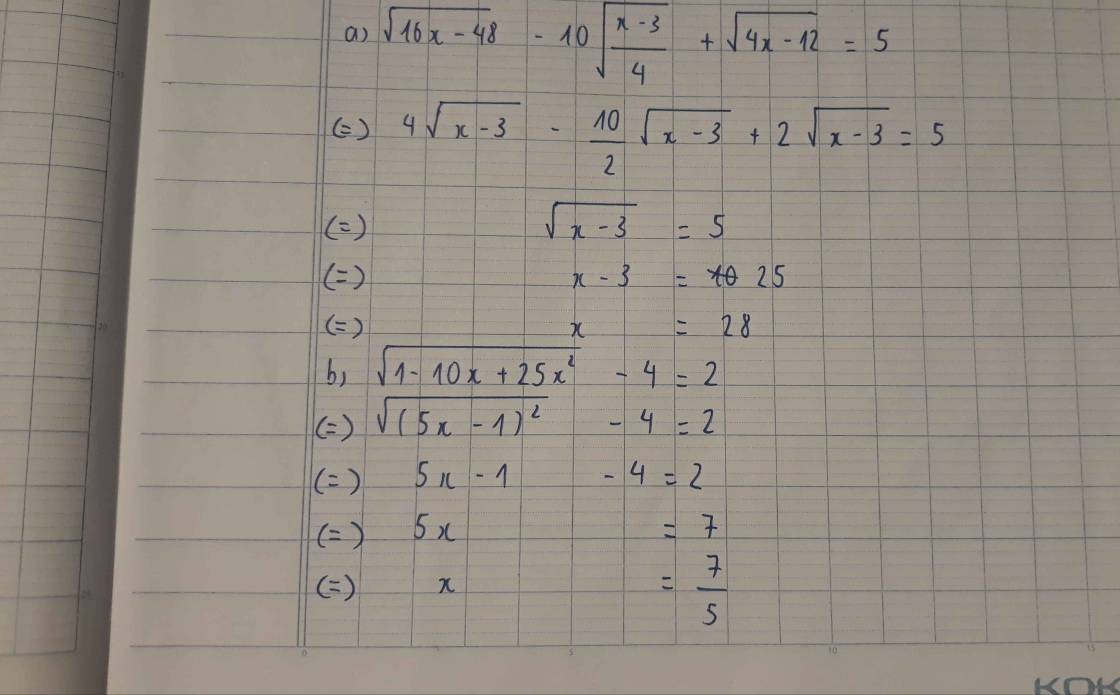a: Đặt \(x^2-4=a\)

Pt sẽ là \(a=3\sqrt{xa}\)

\(\Rightarrow a^2=9xa\)

\(\Leftrightarrow a\left(a-9x\right)=0\)

\(\Leftrightarrow\left(x^2-4\right)\left(x^2-4-9x\right)=0\)

hay \(x\in\left\{2;-2;\dfrac{9+\sqrt{97}}{2};\dfrac{9-\sqrt{97}}{2}\right\}\)

d: Đặt \(\sqrt{x^2-x+1}=a;\sqrt{x^2+x+1}=b\)

Pt sẽ là 2a+b=ab+2

=>(b-2)(1-a)=0

=>b=2 và 1-a

\(\Leftrightarrow\left\{{}\begin{matrix}x^2+x+1=4\\x^2-x+1=1\end{matrix}\right.\Leftrightarrow x\in\varnothing\)

\(x=1\)

\(P=\dfrac{x^4+5x^3-20x^2-27x+30}{x^2+4x-21}\left(1\right)\)

Điều kiện xác định khi và chỉ khi

\(x^2+4x-21\ne0\)

\(\Leftrightarrow x^2+7x-3x-21\ne0\)

\(\Leftrightarrow x\left(x+7\right)-3\left(x+7\right)\ne0\)

\(\Leftrightarrow\left(x-3\right)\left(x+7\right)\ne0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne3\\x\ne-7\end{matrix}\right.\)

Theo đề bài : \(\)

\(x=\sqrt[]{31-12\sqrt[]{3}}=\sqrt[]{27-12\sqrt[]{3}+4}=\sqrt[]{\left(3\sqrt[]{3}-2\right)^2}=\left|3\sqrt[]{3}-2\right|=3\sqrt[]{3}-2\)

\(\left(1\right)\Leftrightarrow P=\dfrac{x^4-3x^3+8x^3-24x^2+4x^2-12x-15x+45-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3\left(x-3\right)+8x^2\left(x-3\right)+4x\left(x-3\right)-15\left(x-3\right)-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{\left(x-3\right)\left(x^3+8x^2+4x-15\right)-15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3+8x^2+4x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^3+7x^2+x^2+7x-3x-15}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{x^2\left(x+7\right)+x\left(x+7\right)-3\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=\dfrac{\left(x^2+x-3\right)\left(x+7\right)+6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

\(\Leftrightarrow P=x^2+x-3+\dfrac{6}{x+7}-\dfrac{15}{\left(x-3\right)\left(x+7\right)}\)

Thay \(x=3\sqrt[]{3}-2\) vào \(P\) ta được

\(\Leftrightarrow P=\left(3\sqrt[]{3}-2\right)^2+3\sqrt[]{3}-2-3+\dfrac{6}{3\sqrt[]{3}-2+7}-\dfrac{15}{\left(3\sqrt[]{3}-2-3\right)\left(3\sqrt[]{3}-2+7\right)}\)

\(\Leftrightarrow P=31-12\sqrt[]{3}+3\sqrt[]{3}-5+\dfrac{6}{3\sqrt[]{3}+5}-\dfrac{15}{\left(3\sqrt[]{3}-5\right)\left(3\sqrt[]{3}+5\right)}\)

\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{\left(3\sqrt[]{3}+5\right)\left(3\sqrt[]{3}-5\right)}-\dfrac{15}{\left(3\sqrt[]{3}\right)^2-5^2}\)

\(\Leftrightarrow P=26-9\sqrt[]{3}+\dfrac{6\left(3\sqrt[]{3}-5\right)}{2}-\dfrac{15}{2}\)

\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+3\left(3\sqrt[]{3}-5\right)\)

\(\Leftrightarrow P=\dfrac{37}{2}-9\sqrt[]{3}+9\sqrt[]{3}-15\)

\(\Leftrightarrow P=\dfrac{37}{2}-15=\dfrac{7}{2}\)

P = 7/2

ĐKXĐ \(3x^2-5x+1\ge0;x^2-2\ge0;x^2-x-1\ge0\)

Ta có : \(\sqrt{3x^2-5x+1}-\sqrt{x^2-2}=\sqrt{3.\left(x^2-x-1\right)}-\sqrt{x^2-3x+4}\)

\(\Leftrightarrow\sqrt{3x^2-5x+1}-\sqrt{3\left(x^2-x-1\right)}=\sqrt{x^2-2}-\sqrt{x^2-3x+4}\)

\(\Leftrightarrow\dfrac{3x^2-5x+1-3.\left(x^2-x-1\right)}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{x^2-2-x^2+3x-4}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)

\(\Leftrightarrow\dfrac{-2x+4}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=\dfrac{3x-6}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\\dfrac{3}{\sqrt{x^2-2}+\sqrt{x^2-3x+4}}+\dfrac{2}{\sqrt{3x^2-5x+1}+\sqrt{3\left(x^2-x-1\right)}}=0\left(∗\right)\end{matrix}\right.\)

Xét phương trình (*) ta có VT > 0 \(\forall x\) mà VP = 0

nên (*) vô nghiệm

Vậy x = 2 là nghiệm phương trình 

Điều kiện xác định phương trình \(x\ge\frac{1}{4}\).

Nhân cả hai vế với \(\sqrt{2}\) phương trình tương đương với

\(\sqrt{4x-2\sqrt{4x-1}}-\sqrt{4x+2\sqrt{4x-1}=4}\leftrightarrow\left|\sqrt{4x-1}-1\right|-\left|\sqrt{4x-1}+1\right|=4\)

\(\leftrightarrow\left|\sqrt{4x-1}-1\right|-\sqrt{4x-1}=5\).

Trường hợp 1. NẾU \(x\ge\frac{1}{2}\to\sqrt{4x-1}-1-\sqrt{4x-1}=5\to\) loại

Trường hợp 2. NẾU \(\frac{1}{4}\le x

a.\(A=\dfrac{x^2-4x+4}{x^3-2x^2-\left(4x-8\right)}=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}=\dfrac{\left(x-2\right)^2}{\left(x^2-4\right)\left(x-2\right)}=\dfrac{x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{1}{x+2}\)

\(A=\dfrac{\left(x-2\right)^2}{x^2\left(x-2\right)-4\left(x-2\right)}\left(x\ne\pm2\right)\\ A=\dfrac{\left(x-2\right)^2}{\left(x-2\right)^2\left(x+2\right)}=\dfrac{1}{x+2}\\ B=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\left(x>0\right)\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+1\right)}{3\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)