lăng trụ tam giác đều ABC.A'B'C' cạnh đáy =a, cạnh bên =a\(\sqrt{2}\). M,N thuộc AB' và A'C sao cho \(\dfrac{AM}{AB'}=\dfrac{A'N}{A'C}=\dfrac{1}{3}\). tính thể tích BMNC'C
Cho lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a, biết A'A=A'B=A'C=a. Tính thể tích khối lăng trụ ABC.A'B'C'.
A. 3 a 3 4
B. a 3 3 4
C. a 3 2 4
D. a 3 4
Đáp án C
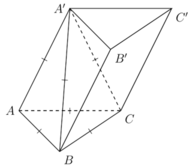
Từ giả thiết suy ra tứ diện A'ABC đều có cạnh a nên có thể tích là
V A ' A B C = a 3 2 12
Khi đó
V A B C . A ' B ' C ' = d A ' , A B C . S A B C = 3 V A ' A B C = a 3 2 4
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A với AB = AC = a, BAC = 120 ° , mặt bên (AB'C') tạ0 với mặt đáy (ABC) một góc 60 ° . Gọi M là điểm thuộc cạnh A'C' sao cho A'M = 3MC'. Tính thể tích V của khối chóp CMBC'
A. V = a 3 32
B. V = a 3 8
C. V = a 3 24
D. V = a 3 8
Chọn A.
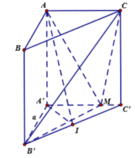
Gọi I là trung điểm của B'C' ![]()
Ta có 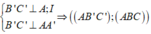

Lại có
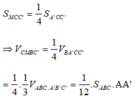
![]()
![]()
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A với AB=AC=a, B A C ^ = 120 o mặt bên (AB'C') tại với mặt đáy (ABC) một góc 60 0 . Gọi M là điểm thuộc cạnh A'C' sao cho A'M=3MC'. Tính thể tích V của khối chóp CMBC'
A. a 3 32
B. a 3 8
C. a 3 24
D. 3 a 3 8
Thể tích khối lăng trụ :cho hình lăng trụ tam giác đều abc.a'b'c' có đáy là tam giác vuông tại b cạnh a'b' hợp với đáy 1 góc 30độ cạnh a'b'=a , a'c'=a căn 2 tính Vabc.a'b'c'
Cho khối lăng trụ ABC.A'B'C' có đáy là các tam giác đều cạnh a, A'A = A'B = A'C = b. Tính thể tích của khối lăng trụ.
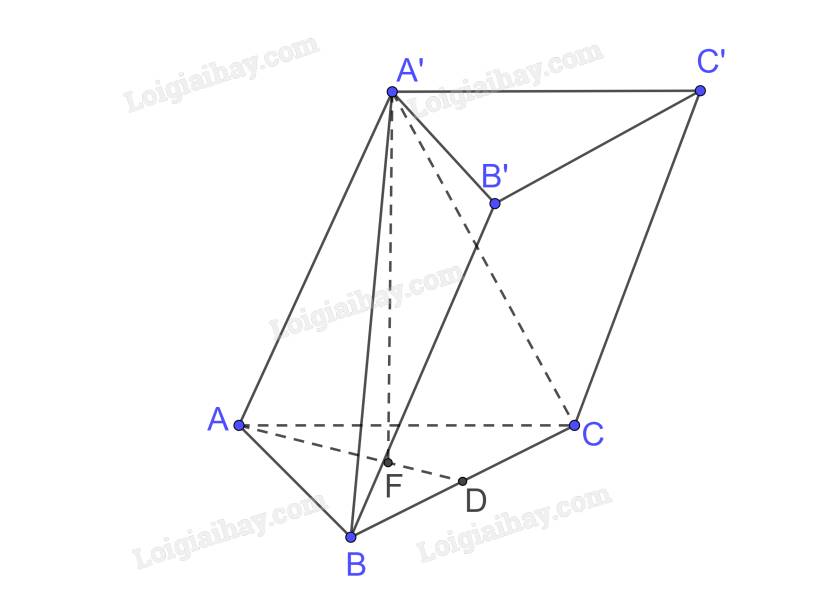
Vì hình chóp A’.ABC có A'A = A'B = A'C và đáy ABC là tam giác đều nên hình chóp A’.ABC đều.
Gọi F là hình chiếu của A’ trên (ABC) nên F là tâm của đáy ABC là tam giác đều do đó F cũng là trọng tâm của tam giác ABC.
Gọi AF cắt BC tại D
Tam giác ABC đều cạnh a nên \(AD = \frac{{a\sqrt 3 }}{2}\)
Mà F là trọng tâm nên \(AF = \frac{2}{3}AD = \frac{{a\sqrt 3 }}{3}\)
Xét tam giác A’AF vuông tại F có
\(A'F = \sqrt {A'{A^2} - A{F^2}} = \sqrt {{b^2} - {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} \)
Diện tích tam giác đều ABC là \(S = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích khối lăng trụ là \(V = A'F.S = \sqrt {{b^2} - \frac{{{a^2}}}{3}} .\frac{{{a^2}\sqrt 3 }}{4}\)
Cho hình lăng trụ tam giác đều ABC.A'B'C' có cạnh bên bằng cạnh đáy. Đường thẳng MN M ∈ A ' C , N ∈ B C ' là đường thẳng vuông góc chung của A'C và BC' . Tỉ số N B N C ' bằng:
A. 5 2 .
B. 3 2 .
C. 2 3 .
D. 1
Đáp án B
Chuẩn hóa AB = 2. Gọi O,H lần lượt là trung điểm cạnh B’C’,BC ⇒ O A ' = 3
Chọn hệ trục tọa độ như hình vẽ
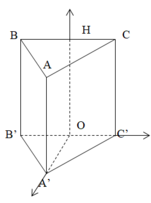
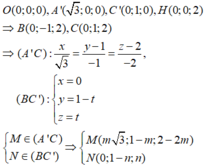
Vì MN là đoạn vuông góc chung của A’C,BC’
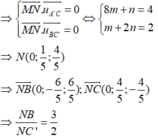
Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a.hình chiếu vuông góc của A' trên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa A'C và mặt phẳng đáy là 60°.tính theo a thể tính hình lăng trụ và khoảng từ B đến mặt phẳng (ACA'C')
Cho lăng trụ ABC.A'B'C' có đáy là tam tác đều cạnh a. Hình chiếu vuông góc của A' lên mặt phẳng (ABC) là trung điểm của cạnh AB, góc giữa đường thẳng A'C và mặt phẳng đáy bằng 60 độ. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách từ điểm B đến mặt phẳn (ACC'A')
Gọi H là trung điểm của AB, \(A'H\perp\left(ABC\right)\) và \(\widehat{A'CH}=60^0\)
Do đó \(A'H=CH.\tan\widehat{A'CH}=\frac{3a}{2}\)
Do đó thể tích khối lăng trụ là \(V_{ABC.A'B'C'}=\frac{3\sqrt{3}a^3}{8}\)
Gọi I là hình chiếu vuông góc của H lên AC; K là hình chiếu vuông góc của H lên A'I. Suy ra :
\(HK=d\left(H,\left(ACC'A'\right)\right)\)
Ta có :
\(HI=AH.\sin\widehat{IAH}=\frac{\sqrt{3}a}{4}\);
\(\frac{1}{HK^2}=\frac{1}{HI^2}+\frac{1}{HA'^2}=\frac{52}{9a^2}\)
=>\(HK=\frac{3\sqrt{13}a}{26}\)
Do đó \(d\left(B;\left(ACC'A'\right)\right)=2d\left(H;\left(ACC'A'\right)\right)=2HK=\frac{3\sqrt{13}a}{13}\)
Cho hình lăng trụ A B C . A ' B ' C ' có mặt đáy là tam giác đều cạnh A B = 2 a . Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 ° . Góc giữa đường thẳng A'C và (ABC) là
A. π 4
B. π 3
C. a r c sin 1 4
D. π 6