Chọn A.
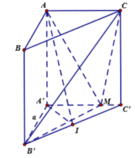
Gọi I là trung điểm của B'C' ![]()
Ta có 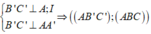

Lại có
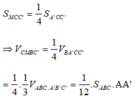
![]()
![]()
Chọn A.

Gọi I là trung điểm của B'C' ![]()
Ta có 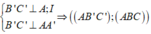

Lại có
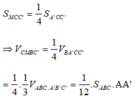
![]()
![]()
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân ABC với AB=AC=2x, B A C ⏜ = 120 0 , mặt phẳng (AB'C') tạo với đáy một góc 30 0 . Tính thể tích V của khối lăng trụ đã cho?
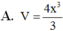
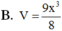
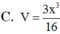
![]()
Cho khối lăng trụ đứng ABCD.A'B'C'D' có đáy là tam giác cân ABC với AB=AC=a, B A C ⏜ = 120 0 mặt phẳng (AB'C') tạo với đáy một góc 30 0 .Tính thể tích V của khối lăng trụ đã cho.
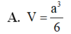
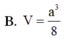
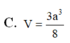
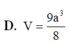
Cho khối lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân với AB=AC=a, B A C ⏜ = 120 0 , mặt phẳng (A'B'C') tạo với đáy một góc 60 0 . Tính thể tích V của khối lăng trụ đã cho
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông cân tại A, cạnh BC = a√6. Góc giữa mặt phẳng (AB'C) và mặt phẳng (BCC'B') bằng 600. Tính thể tích V của khối lăng trụ ABC.A'B'C'?
A . V = 2 a 3 3 3
B . V = a 3 3 2
C . V = 3 a 3 3 4
D . V = 3 a 3 3 2
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại C, BAC = 30 ° , AB = a 3 , AA' = a. Gọi M là trung điểm của BB'. Tính theo a thể tích V của khối tứ diện MACC'.
A. V = a 3 3 12
B. V = a 3 3 4
C. V = a 3 3 3
D. V = a 3 3 18
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác vuông tại A với AB = a, AC = a 3 . Hình chiếu vuông góc của A' lên mặt phẳng (ABC) trùng với trọng tâm G của tam giác ABC và góc giữa AA’ tạo với mặt phẳng (ABC) bằng 60 ∘ . Gọi V là thể tích khối lăng trụ ABC.A'B'C'. Tính V 3 + V a 3 - 1 .
A. 1.
B. a.
C. a 2 .
D. a 3 .
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông cân tại A, mặt bên BCC'B' là hình vuông cạnh 2a. Tính thể tích V của khối lăng trụ ABC.A'B'C'.
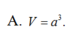
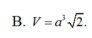
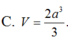
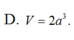
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, A C B ⏜ , b'c tạo với mặt phẳng AA'B'C' một góc 30 0 . Tính thể tích V của khối lăng trụ ABC.A'B'C'.
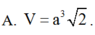
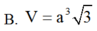
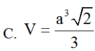

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, B A C ^ = 120 o và BC =AA' = a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'.
A. V = 9 a 3 4
B. V = 3 3 a 3 6
C. V = 3 3 a 3 2
D. V = 3 a 3 4