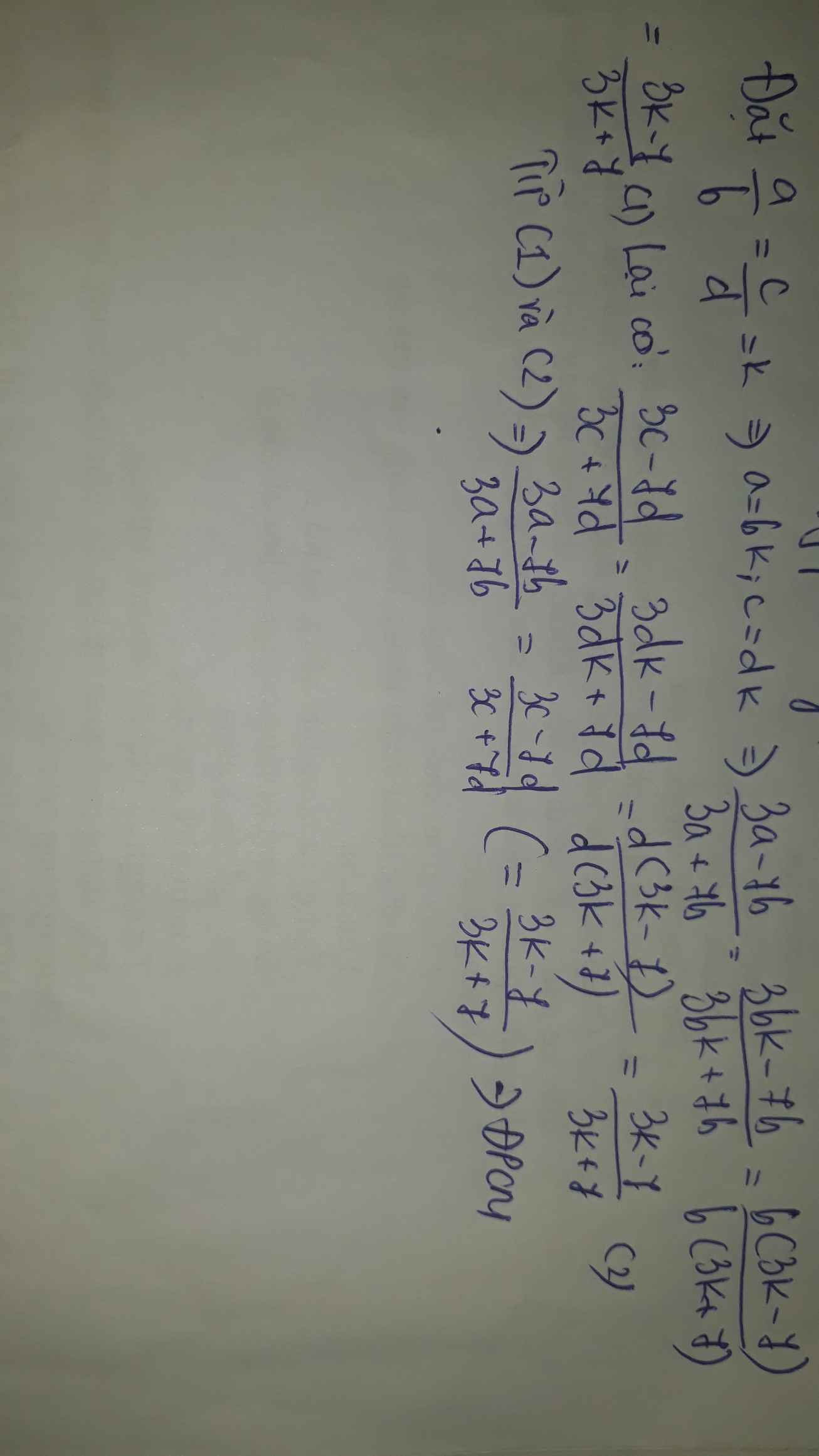Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

=>\(a=bk;c=dk\)

1: \(\dfrac{2a+3c}{2b+3d}=\dfrac{2\cdot bk+3\cdot dk}{2b+3d}=\dfrac{k\left(2b+3d\right)}{2b+3d}=k\)

\(\dfrac{2a-3c}{2b-3d}=\dfrac{2bk-3dk}{2b-3d}=\dfrac{k\left(2b-3d\right)}{2b-3d}=k\)

Do đó: \(\dfrac{2a+3c}{2b+3d}=\dfrac{2a-3c}{2b-3d}\)

2: \(\dfrac{4a-3b}{4c-3d}=\dfrac{4\cdot bk-3b}{4\cdot dk-3d}=\dfrac{b\left(4k-3\right)}{d\left(4k-3\right)}=\dfrac{b}{d}\)

\(\dfrac{4a+3b}{4c+3d}=\dfrac{4bk+3b}{4dk+3d}=\dfrac{b\left(4k+3\right)}{d\left(4k+3\right)}=\dfrac{b}{d}\)

Do đó: \(\dfrac{4a-3b}{4c-3d}=\dfrac{4a+3b}{4c+3d}\)

3: \(\dfrac{3a+5b}{3a-5b}=\dfrac{3bk+5b}{3bk-5b}=\dfrac{b\left(3k+5\right)}{b\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\)

\(\dfrac{3c+5d}{3c-5d}=\dfrac{3dk+5d}{3dk-5d}=\dfrac{d\left(3k+5\right)}{d\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\)

Do đó: \(\dfrac{3a+5b}{3a-5b}=\dfrac{3c+5d}{3c-5d}\)

4: \(\dfrac{3a-7b}{b}=\dfrac{3bk-7b}{b}=\dfrac{b\left(3k-7\right)}{b}=3k-7\)

\(\dfrac{3c-7d}{d}=\dfrac{3dk-7d}{d}=\dfrac{d\left(3k-7\right)}{d}=3k-7\)

Do đó: \(\dfrac{3a-7b}{b}=\dfrac{3c-7d}{d}\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

\(\Leftrightarrow\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)

\(\dfrac{2a+3c}{3a+4c}=\dfrac{2bk+3dk}{3bk+4dk}=\dfrac{2b+3d}{3b+4d}\)

a, Áp dụng t/c dtsbn:

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)

b, Áp dụng t/c dtsbn:

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)

c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)

Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)

\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)

Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)

d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)

Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)

\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)

Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)

\(=\dfrac{11a+17b}{11c-17d}=\dfrac{3a-4b}{3c-4d}\)

\(\Rightarrow...\)

Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)

\(\Rightarrow a=bk,c=dk\)

\(\Rightarrow\dfrac{11a+17b}{3a-4b}=\dfrac{11bk+17b}{3bk-4b}=\dfrac{b\left(11k+17\right)}{b\left(3k-4\right)}=\dfrac{11k+17}{3k-4}\left(1\right)\)

\(\Rightarrow\dfrac{11c+17d}{3c-4d}=\dfrac{11dk+17d}{3dk-4d}=\dfrac{d\left(11k+17\right)}{d\left(3k-4\right)}=\dfrac{11k+17}{3k-4}\left(2\right)\)

Từ (1) và (2) \(\Rightarrow\dfrac{11a+17b}{3a-4b}=\dfrac{11c+17d}{3c-4d}\)

Bài 1:

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk\)

Khi đó: \(\left\{\begin{matrix} \frac{2a+5b}{3a-4b}=\frac{2bk+5b}{3bk-4b}=\frac{b(2k+5)}{b(3k-4)}=\frac{2k+5}{3k-4}\\ \frac{2c+5d}{3c-4d}=\frac{2dk+5d}{3dk-4d}=\frac{d(2k+5)}{d(3k-4)}=\frac{2k+5}{3k-4}\end{matrix}\right.\)

\(\Rightarrow \frac{2a+5b}{3a-4b}=\frac{2c+5d}{3c-4d}\)

Ta có đpcm.

Bài 2:

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk\)

Khi đó: \(\frac{ab}{cd}=\frac{bk.b}{dk.d}=\frac{b^2}{d^2}\)

\(\frac{a^2+b^2}{c^2+d^2}=\frac{(bk)^2+b^2}{(dk)^2+d^2}=\frac{b^2(k^2+1)}{d^2(k^2+1)}=\frac{b^2}{d^2}\)

Do đó: \(\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}(=\frac{b^2}{d^2})\) . Ta có đpcm.

Bài 3:

a) Sửa điều kiện: \(\frac{a}{b}=\frac{c}{d}\neq -1\)

Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk; c=dk\)

Theo đkđb thì \(k\neq -1\) nên \(k^3+1\neq 0\); \(k+1\neq 0\)

Ta có: \(\frac{a^3+b^3}{c^3+d^3}=\frac{(bk)^3+b^3}{(dk)^3+d^3}=\frac{b^3(k^3+1)}{d^3(k^3+1)}=\frac{b^3}{d^3}\)

\(\frac{(a+b)^3}{(c+d)^3}=\frac{(bk+b)^3}{(dk+d)^3}=\frac{b^3(k+1)^3}{d^3(k+1)^3}=\frac{b^3}{d^3}\)

\(\Rightarrow \frac{a^3+b^3}{c^3+d^3}=\frac{(a+b)^3}{(c+d)^3}\) (đpcm)

b)

Đặt \(\frac{a}{b}=k; \frac{c}{d}=t\Rightarrow a=bk; c=dt\)

Ta cần cm \(k=t\)

Khi đó:

\(\frac{2a+13b}{3a-7b}=\frac{2bk+13b}{3bk-7b}=\frac{b(2k+13)}{b(3k-7)}=\frac{2k+13}{3k-7}\)

\(\frac{2c+13d}{3c-7d}=\frac{2dt+13d}{3dt-7d}=\frac{d(2t+13)}{d(3t-7)}=\frac{2t+13}{3t-7}\)

Vì \(\frac{2a+13b}{3a-7b}=\frac{2c+13d}{3c-7d}\Rightarrow \frac{2k+13}{3k-7}=\frac{2t+13}{3t-7}\)

\(\Rightarrow (2k+13)(3t-7)=(2t+13)(3k-7)\)

\(-14k+39t=-14t+39k\Rightarrow k=t\)

Ta có đpcm.

Lời giải:

Đặt $\frac{a}{b}=\frac{c}{d}=k$

$\Rightarrow a=bk, c=dk$

Khi đó:

$\frac{2a+3b}{3a-5b}=\frac{2bk+3b}{3bk-5b}=\frac{b(2k+3)}{b(3k-5)}=\frac{2k+3}{3k-5}(1)$

$\frac{2c+3d}{3c-5d}=\frac{2dk+3d}{3dk-5d}=\frac{d(2k+3)}{d(3k-5)}=\frac{2k+3}{3k-5}(2)$

Từ $(1); (2)$ ta có đpcm.