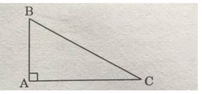
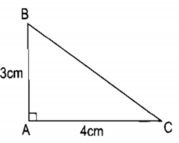
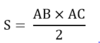Cho biết công thức tính diện tích tam giác vuông ABC với AB, AC là các cạnh góc vuông là \(S_{ABC}=\dfrac{1}{2}AC.AB\). Sử dụng công thức này (Không sử dụng công thức tính diện tích của các hình khác) để chứng minh rằng:
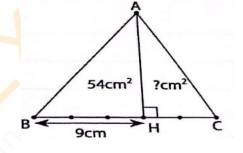
- Diện tích tam giác A'B'C' với B'C' là đáy, A'H' là đường cao là\(S_{A'B'C'}=\dfrac{1}{2}B'C'.A'H'\)
- Diện tích hình chữ nhật A''B''C''D'' với A''B'' là chiều dài, B''C'' là chiều rộng là\(S_{A''B''C''D''}=A''B''.B''C''\)
- Diện tích hình bình hành EFGH với EF là đáy, EH là chiều cao là \(S_{EFGH}=EF.EH\)
- Diện tích hình thang E'F'G'H' với E'F' là đáy bé, G'H' là đáy lớn, E'I' là chiều cao là \(S_{E'F'G'H'}=\dfrac{1}{2}\left(E'F'+G'H'\right)E'I'\)
-Diện tích hình tứ giác MNPQ có hai đường chéo \(MP\perp NQ\) là \(S_{MNPQ}=\dfrac{1}{2}MP.NQ\)
Bạn nào giải đúng mình sẽ tặng 1SP
CHÚC CÁC BẠN HỌC GIỎI..........