Phương trình này vô nghiệm có đúng không ạ

Những câu hỏi liên quan
Giúp mình 2 câu này với ạ:
1. Tìm m để bất phương trình sau có nghiệm đúng với mọi x :
mx2 +(m+1)x+m-1 <0
2. Tìm m để bất phương trình sau vô nghiệm :
mx2-4(m+1)x+m-5<0
1.
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta=\left(m+1\right)^2-4m\left(m-1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\-3m^2+7m+1< 0\end{matrix}\right.\)
\(\Leftrightarrow m< \dfrac{7-\sqrt{61}}{6}\)
2.
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\3m^2+13m+4\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4\le m\le-\dfrac{1}{3}\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Đúng 4
Bình luận (3)
Cho phương trình
(
m
2
+
1
)
(
x
2
-
3
x
+
2
)
2011
-
3
x
+
4
0Các phát biểu :(1) Phương trình trên vô nghiệm vơi mọi m(2) Khi m 1 phương trình trên có nghiệm(3) Không tồn tại m để phương trình trên vô nghiệmChọn đáp án đúng: A. (1) đúng B. (2),(3) Đúng C. A, B đ...
Đọc tiếp
Cho phương trình ( m 2 + 1 ) ( x 2 - 3 x + 2 ) 2011 - 3 x + 4 = 0
Các phát biểu :
(1) Phương trình trên vô nghiệm vơi mọi m
(2) Khi m = 1 phương trình trên có nghiệm
(3) Không tồn tại m để phương trình trên vô nghiệm
Chọn đáp án đúng:
A. (1) đúng
B. (2),(3) Đúng
C. A, B đều đúng
D. Tất cả đều sai.
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau? 1. Phương trình vô nghiệm trên trường số thực R. 2. Phương trình vô nghiệm trên trường số phức C 3. Phương trình không có nghiệm thuộc tập số thực. 4. Phương trình có bốn nghiệm thuộc tập số phức. 5. Phương trình chỉ có hai nghiệm là số phức. 6. Phương trình có hai nghiệm là số thực A. 0. B. 1. C. 3. D. 2.
Đọc tiếp
Trên tập số phức, cho phương trình sau : ( z + i)4 + 4z2 = 0. Có bao nhiêu nhận xét đúng trong số các nhận xét sau?
1. Phương trình vô nghiệm trên trường số thực R.
2. Phương trình vô nghiệm trên trường số phức C
3. Phương trình không có nghiệm thuộc tập số thực.
4. Phương trình có bốn nghiệm thuộc tập số phức.
5. Phương trình chỉ có hai nghiệm là số phức.
6. Phương trình có hai nghiệm là số thực
A. 0.
B. 1.
C. 3.
D. 2.
Chọn D.
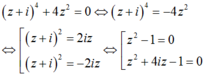
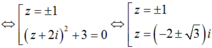
Do đó phương trình có 2 nghiệm thực và 4 nghiệm phức. Vậy nhận xét 4, 6 đúng.
Đúng 0
Bình luận (0)
Với những dạng bài giải phương trình/bất phương trình mà có kết quả như thế này thì kết luận sao ạ?
\(0=0\) (luôn đúng)
\(-1>0\) (vô lí)
0=0 thì pt thoả mãn với mọi x
-1>0 pt vô nghiệm \(S=\varnothing\)
Đúng 3
Bình luận (0)
`1.` Với `0=0(` luôn đúng `)` `->` Kết luận: Vậy `S={x|x\inRR}`
`2.` Với `-1>0(` vô lý `)` `->` Kết luận: Vậy `S=∅`
Đúng 1
Bình luận (0)
Cho bất phương trình 2x+y>3. Khẳng định nào sau đây là đúng?
A. Bất phương trình đã cho có nghiệm duy nhất
B. Bất phương trình đã cho vô nghiệm
C. Bất phương trình đã cho có vô số nghiệm
D. Bất phương trình đã cho có tập nghiệm là \(\left[ {3; + \infty } \right)\)
Bất phương trình 2x+y > 3 là bất phương trình bậc nhất hai ẩn và có vô số nghiệm.
Chọn C.
Đúng 0
Bình luận (0)
Cho hệ phương trình
7
x
-
5
y
9
14
x
-
...
Đọc tiếp
Cho hệ phương trình
7 x - 5 y = 9 14 x - 10 y = 10
Tại sao không cần giải ta cũng kết luận được hệ phương trình này vô nghiệm.
Ta có:
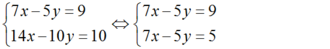
Không tồn tại cặp nghiệm (x ; y) nào thỏa mãn hệ phương trình trên nên hệ phương trình đã cho vô nghiệm.
Đúng 0
Bình luận (0)
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau: Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu. Bước 2: Với điều kiện a, c trái dấu ta có a.c 0 suy ra Δ b2 - 4ac 0. Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm. Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu. Lập luận trên sai từ bước nào? A. Bước 1 B. Bước 2 C. Bước 3 D. Bước 4.
Đọc tiếp
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c = 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau:
Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu.
Bước 2: Với điều kiện a, c trái dấu ta có a.c > 0 suy ra Δ = b2 - 4ac > 0.
Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.
Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu.
Lập luận trên sai từ bước nào?
A. Bước 1
B. Bước 2
C. Bước 3
D. Bước 4.
Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.
Đúng 0
Bình luận (0)
Phương trình
(
m
4
+
m
+
1
)
x
2011
+
x
5
-
32
0
(1) Phương trình trên có ít nhất một nghiệm dương với mọi giá trị của m.(2) Phương trình trên vô nghiệm(3) Phương trình trên có nghiệm với mọi mChọn đáp án đúng A. Cả 3 đều sai B. Cả 3 đều đúng C. Chỉ có (1) đúng D. (1),(3) Đúng
Đọc tiếp
Phương trình ( m 4 + m + 1 ) x 2011 + x 5 - 32 = 0
(1) Phương trình trên có ít nhất một nghiệm dương với mọi giá trị của m.
(2) Phương trình trên vô nghiệm
(3) Phương trình trên có nghiệm với mọi m
Chọn đáp án đúng
A. Cả 3 đều sai
B. Cả 3 đều đúng
C. Chỉ có (1) đúng
D. (1),(3) Đúng
cho phương trình \(x^4-2\left(m+1\right)x^2+m-2=0\) Tìm m để:
a) Phương trình đã cho có 4 nghiệm phân biệt.
b) Phương trình đã cho vô nghiệm.
c) Phương trình đã cho có đúng hai nghiệm.
Đặt \(x^2=t\) phương trình trở thành:
\(t^2-2\left(m+1\right)t+m-2=0\) (1)
a. Phương trình có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=\left(m+1\right)^2-\left(m-2\right)>0\\t_1+t_2=2\left(m+1\right)>0\\t_1t_2=m-2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2+m+3>0\left(\text{luôn đúng}\right)\\m>-1\\m>2\end{matrix}\right.\)
\(\Rightarrow m>2\)
b. Do \(\Delta'=m^2+m+3>0;\forall m\) nên pt đã cho vô nghiệm khi (1) có 2 nghiệm pb đều âm
\(\Rightarrow\left\{{}\begin{matrix}t_1+t_2=2\left(m+1\right)< 0\\t_1t_2=m-2>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m< -1\\m>2\end{matrix}\right.\) \(\Rightarrow\) không tồn tại m thỏa mãn
c. Pt có đúng 2 nghiệm khi (1) có 2 nghiệm trái dấu
\(\Leftrightarrow t_1t_2=m-2< 0\Rightarrow m< 2\)
Đúng 2
Bình luận (0)















