Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của z , biết z là số phức thỏa mãn z − i = 2 .
A. z min = 1 ; z max = 3 .
B. z min = 3 ; z max = 9 .
C. z min = 1 ; z max = 9 .
D. z min = 0 ; z max = 3 .
Đáp án A
Gọi z = x + i y ; x , y ∈ ℝ .
z − i = 2 ⇔ x + i y − i = 2 ⇔ x 2 + y − 1 2 = 4 ⇒ x 2 + y 2 = 2 y + 3
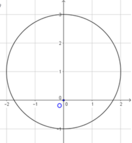
Do đó tập hợp các số phức z là đường tròn tâm I(0;1), bán kính R=2 (như hình vẽ).
z = x 2 + y 2 = 2 y + 3 , − 1 ≤ y ≤ 3 − 2 ≤ x ≤ 2 .
Dễ thấy,
z min = 2 − 1 + 3 = 1 ; z max = 2.3 + 3 = 3.
Các bạn chỉ cho mình từng dấu công nhá
+ Nếu mà 1 bài khong phân bietj rõ ra là tìm GTLN và GTNN thì làm sao để biết được câu nào là GTLN câu ào là giá trị nhỏ nhất ạ !
+ Khi mà tìm ra GTLN và GTNN ví dụ như (x+3/2)^2 + 3 >=3 . Thì khi tìm tại x bằng bao nhiêu thì tại sao chỉ lấy mỗi x+3/2 thôi mà không lấy cả (x+3/2)^2 + 3 = 0 ạ ( Số +3) đó tại sao không được cho vào để tìm khi x bằng bao nhiêu ạ
+1 còn tùy vào từng loại cần tìm nếu đơn giản là đa thức bậc 2 thì sử dụng máy tính hoặc cứ tìm thôi ;-;
+2 Vì \(m^2+3\ge3\) thì để dấu = xảy ra tức là : \(m^2+3=3\) \(\Leftrightarrow m^2=0\)
<=> m = 0 .
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Cho biểu thức 4x+9/x-1
a, B có giá trị nhỏ nhất. Tìm GTNN
b, B có GTLN. Tìm GTLN
a)Cho biểu thức A=|x-3|+5 có giá trị nhỏ nhất (GTNN). Tìm GTNN đó
b)Cho biểu thức B=20-|x+2| có giá trị lớn nhất (GTLN) . Tìm GTLN đó
tìm GTLN ( hoặc nhỏ nhất) của đa thức sau
(x-1)^2+3 1-x^2
\(a,\) Ta có: \(\left(x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^2+3\ge3\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x-1=0\Leftrightarrow x=1\)
Vậy \(GTNN\) của đa thức là \(3\) khi \(x=1.\)
\(b,\) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow-x^2\le0\forall x\)
\(\Rightarrow1-x^2\le1\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x^2=0\Leftrightarrow x=0\)
#\(Toru\)
Đặt A = (x - 1)² + 3
Do (x - 1)² ≥ 0 với mọi x ∈ R
⇒ (x - 1)² + 3 ≥ 3 với mọi x ∈ R
Vậy GTNN của A là 3 khi x = 1
---------------
Đặt B = 1 - x² = -x² + 1
Do x² ≥ 0 với mọi x ∈ R
⇒ -x² ≤ 0 với mọi x ∈ R
⇒ -x² + 1 ≤ 1 với mọi x ∈ R
Vậy GTLN của B là 1 khi x = 0
Bài 1 : y=2(x2+x+1)x2+1y=2(x2+x+1)x2+1
Tìm GTLN ( giá trị lớn nhất ) và GTNN( giá trị nhỏ nhất) của hàm số
Tìm GTLN(GTNN) của biểu thức (nếu có) [GTLN: giá trị lớn nhất ; GTNN:giá trị nhỏ nhất]
\(A=-3,7-\left|1,7-m\right|\)
giúp tui :;;; xin cảm ơn TwT | ^_^
ok luôn bài này là max nhé :
\(A=-3,7-\left|1,7-m\right|\le-3,7\forall m\) (vì : \(\left|1,7-m\right|\ge0\forall m\) )
" = " <=> m = 1,7
Vậy ...
B1Tìm GTLN
a) 2+|x+3|
b) 3/2+|2x-1|
B2 Cho biểu thức A=3|a|+2/4|a|-5
Tìm a thuộc Z để a đạt GTLN, tìm GTLN đó
P/s: GTLL: GIÁ TRỊ LỚN NHẤT
GTNN: GIÁ TRỊ NHỎ NHẤT
Ai làm được thanh kiu
\(a)A=2+|x+3|\)
Vì \(|x+3|\ge0\)\(\forall x\)
\(\Rightarrow2+|x+3|\ge2\)\(\forall x\)
Dấu "=" xảy ra:
\(\Leftrightarrow x+3=0\)
\(\Leftrightarrow x=-3\)
Vậy \(Max_A=2\Leftrightarrow x=-3\)
\(b)B=\frac{3}{2}+|2x-1|\)
Vì \(|2x-1|\ge0\)\(\forall x\)
\(\Rightarrow\frac{3}{2}+|2x-1|\ge\frac{3}{2}\)\(\forall x\)
Dấu "=" xảy ra:
\(\Leftrightarrow2x-1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy \(Max_B=\frac{3}{2}\Leftrightarrow x=\frac{1}{2}\)
Tìm GTLN hoặc nhỏ nhất của biểu thức Sau
\(-4x^2+5x-21\)
\(-4x^2+5x-21\)
\(=-4\left(x^2-\frac{5}{4}x\right)-21\)
\(=-4\left(x^2-2x.\frac{5}{8}+\frac{25}{64}\right)-21+\frac{25}{16}\)
\(=-4\left(x-\frac{5}{8}\right)^2-\frac{311}{16}\)
Có \(\left(x-\frac{5}{8}\right)^2\ge0\) với mọi x
=> \(-4\left(x-\frac{5}{8}\right)^2\le0\)với mọi x
=> \(-4\left(x-\frac{5}{8}\right)^2-\frac{311}{16}\le\frac{-311}{16}\)với mọi x
Dấu "=" xảy ra <=> \(x-\frac{5}{8}=0\)<=> \(x=\frac{5}{8}\)
KL: GTLN của biểu thức là \(\frac{-311}{16}\)<=> \(x=\frac{5}{8}\)
\(A=-4x^2+5x-21\)
\(=-\left[\left(2x\right)^2-2\times2x\times\frac{5}{4}+\left(\frac{5}{4}\right)^2-\left(\frac{5}{4}\right)^2+21\right]\)
\(=-\left[\left(2x-\frac{5}{4}\right)^2+\frac{311}{16}\right]\)
\(\left(2x-\frac{5}{4}\right)^2\ge0\)
\(\left(2x-\frac{5}{4}\right)^2+\frac{311}{16}\ge\frac{311}{16}\)
\(-\left[\left(2x-\frac{5}{4}\right)^2+\frac{311}{16}\right]\le-\frac{311}{16}\)
Vậy Max A = \(-\frac{311}{16}\) khi x = \(\frac{5}{8}\)
