Cho các số thực a ; b ; c ; d ; e khác 0 thỏa mãn: \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=\dfrac{d}{e}\)
Chứng minh rằng: \(\dfrac{2a^4+3b^4+4c^4+5d^4}{2b^4+3c^4+4d^4+5e^4}=\dfrac{a}{e}\)
Những câu hỏi liên quan
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 18:58
a) Tìm tất cả các số thực x sao cho x2 = 4.
b) Tìm tất cả các số thực x sao cho x3 = - 8.
a) \({x^2} = 4 = {2^2} = {\left( { - 2} \right)^2} \Leftrightarrow x = \pm 2\)
b) \({x^3} = - 8 = {\left( { - 2} \right)^3} \Leftrightarrow x = - 2.\)
- Chú ý:
Trong toán học, căn bậc chẵn của một số là một số lớn hơn 0. Do đó số âm không có căn bậc chẵn.
Đúng 0
Bình luận (0)
Cho các mệnh đề sau:(I). Nếu
a
b
c
t
h
ì
2
ln
a
ln
b
+
ln
c
(II). Cho số thực 0 a ≠ 1. Khi đó
a
-
1
log
a
x
≥
0...
Đọc tiếp
Cho các mệnh đề sau:
(I). Nếu a = b c t h ì 2 ln a = ln b + ln c
(II). Cho số thực 0 < a ≠ 1. Khi đó a - 1 log a x ≥ 0 ⇔ x ≥ 1
(III). Cho các số thực 0 < a ≠ 1 , b > 0 , c > 0 . Khi đó b log a c ≥ 0 ⇔ x ≥ 1
(IV). l i m x → + ∞ 1 2 x = - ∞ .
Số mệnh đề đúng trong các mệnh đề trên là
A. 3
B. 4
C. 2
D. 1
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:
Đúng 0
Bình luận (0)
Xác định INPUT, OUTPUT của các bài toán sau:
Tìm giá trị tuyệt đối của 1 số nguyên a cho trước.
Tính tổng các phần tử dương của dãy n số thực cho trước.
Tính số các số chẵn trong dãy n số thực cho trước
Tính Tổng 50 số tự nhiên đầu tiên
. Giup m z nhae
Cho các số tự nhiên 12,46,81,31
a, Tìm tất cả các ước thực sự của mỗi số
b, tì tổng của các ước thực sự của mỗi số
Cho số thực x thỏa mãn
log
x
1
2
log
3
a
-
2
log
b
+
3
log
c
(a,b,c là các số thực dương). Hãy biểu diễn x theo a, b, c. A.
x
c
3
3
a
b...
Đọc tiếp
Cho số thực x thỏa mãn log x = 1 2 log 3 a - 2 log b + 3 log c (a,b,c là các số thực dương). Hãy biểu diễn x theo a, b, c.
A. x = c 3 3 a b 2
B. x = 3 a b 2 c 3
C. x = 3 a c b 2
D. x = 3 a c 3 b 2
Xét phương trình
a
x
3
−
x
2
+
b
x
−
1
0
với a, b là các số thực,
a
≠
0
,
a
≠
b
sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2...
Đọc tiếp
Xét phương trình a x 3 − x 2 + b x − 1 = 0 với a, b là các số thực, a ≠ 0 , a ≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 − 3 a b + 2 a 2 b − a .
A. 15 3 .
B. 8 2 .
C. 11 6 .
D. 12 3 .
Cho các số thực a, b thỏa mãn a − 2b và 3a + 4b đều là các số hữu tỷ. Chứng minh a, b đều là các số hữu tỷ.
Cho các số thực a, b thỏa mãn a − 2b và 3a + 4b đều là các số hữu tỷ. Chứng minh a, b đều là các số hữu tỷ.
Cho a là số thực dương khác 1 và x,y là các số thực dương. Mệnh đề nào dưới đây đúng? A.
log
a
a
3
3
B.
log
a
(
x
2
y
)...
Đọc tiếp
Cho a là số thực dương khác 1 và x,y là các số thực dương. Mệnh đề nào dưới đây đúng?
A. log a a 3 = 3
B. log a ( x 2 y ) = 2 log a x log a y
C. log a ( xy ) - log a y = log a x
D. log a xlog a y = log a ( xy )
Xét phương trình ax3- x2+ bx-10 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức
P
5
a
2
-
3
a
b
+
2
a
2
(
b
-...
Đọc tiếp
Xét phương trình ax3- x2+ bx-1=0 với a, b là các số thực a≠0; a≠ b sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức P = 5 a 2 - 3 a b + 2 a 2 ( b - a ) .
A. 15 3
B. 8 2
C. 11 6
D. 12 3
Giả sử phương trình đã cho có 3 nghiệm
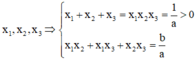
Khi đó
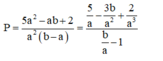
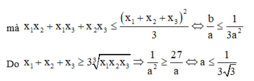
Suy ra
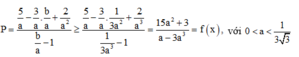
Xét hàm số:
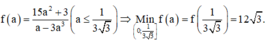
Chọn D.
Đúng 0
Bình luận (0)