Cho 2 điểm phân biệt A, B, điểm O không thuộc AB. CMR với mọi điểm M đều có cặp số (x; y), x + y = 1 sao cho \(\overrightarrow{OM}=x.\overrightarrow{OA}+y.\overrightarrow{OB}\)

Những câu hỏi liên quan
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a, b tương ứng song song với m, n (H.7.2).a) Mỗi cặp đường thẳng a, a và b, b có cùng thuộc một mặt phẳng hay không?b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO cắt a tại A, đường thẳng qua B song song với OO cắt b tại B Giải thích vì sao OAAO, OBBO, ABBA là các hình bình hành.c) So sánh góc giữa hai đường thẳng a, b và góc giữa...
Đọc tiếp
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).
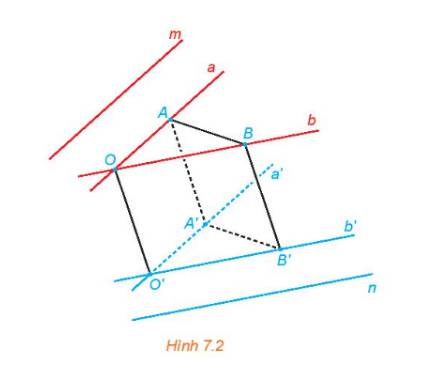
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.
(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a', b // b'.
b) Ta có:
+) OA // O′A′; OO' // AA' nên OAA'O' là hình bình hành.
+) OB // O′B′; OO' // BB' nên OBB'O' là hình bình hành.
+) AB // A′B′ và OO' // AA' OO' // BB' suy ra AA' // BB' nên ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(\cos \left( {a,b} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}};\cos \left( {a',b'} \right) = \frac{{O'{{A'}^2} + O'{{B'}^2} - A'{{B'}^2}}}{{2.O'A'.O'B'}}\)
Vì O'A' = OA và O'B' = OB; AB = A'B' nên cos(a,b) = cos(a′,b′).
Đúng 0
Bình luận (0)
1 . Cho đường tròn (O;13 cm) , dây AB24cma) Tính khoảng cách từ tâm O đến dây AB?b) Gọi M là điểm thuộc dây AB. Qua M, vẽ dây CD vuông góc với dây AB tại điểm M. Xác định vị trí điểm M trên dây AB để ABCD2 . Cho đường tròn (O) và 2 điểm A,B phân biệt thuộc (O) sao cho đường thẳng AB không đi qua tâm O trên tia đối của tia AB lấy điểm M khác điểm A, từ điểm M kẻ 2 tiếp tuyến phân biệt M E ,MF với đường tròn .GỌI H là trung điểm của dây cung AB , các điểm K và I theo thứ tự là giao điểm của đường...
Đọc tiếp
1 .
Cho đường tròn (O;13 cm) , dây AB=24cm
a) Tính khoảng cách từ tâm O đến dây AB?
b) Gọi M là điểm thuộc dây AB. Qua M, vẽ dây CD vuông góc với dây AB tại điểm M. Xác định vị trí điểm M trên dây AB để AB=CD
2 .
Cho đường tròn (O) và 2 điểm A,B phân biệt thuộc (O) sao cho đường thẳng AB không đi qua tâm O trên tia đối của tia AB lấy điểm M khác điểm A, từ điểm M kẻ 2 tiếp tuyến phân biệt M E ,MF với đường tròn .GỌI H là trung điểm của dây cung AB , các điểm K và I theo thứ tự là giao điểm của đường thẳng EF với các đường thẳng OM
1 cm m,o,h,e,f cùng nằm trên 1 đường tròn
2 oh .oi=ok.om
3Cm IA,IB là các tiếp tuyến của đường tròn
Vẽ 5 điểm A , B , C , M và N trong đó ba điểm A , B , C thẳng hàng , ba điểm A , B , M không thẳng hàng , ba điểm A , B , N thẳng hàng a) Chứng tỏ bốn điểm A , B , C và N cùng 1đường thẳng ( giả sử đó là đường thẳng d )b) Trong cách viết sau , cách nào đùng cách nào saiA thuộc dB không thuộc dM thuộc dN không thuộc dc ) Hai đường thẳng AN và BC có là 2 đường thẳng phân biệt không ?Hai đường thẳng AB và MN có là 2 đường thẳng trùng nhau không ?d ) Có bao nhiêu đường thẳng đi qua từng cặp 2 đi...
Đọc tiếp
Vẽ 5 điểm A , B , C , M và N trong đó ba điểm A , B , C thẳng hàng , ba điểm A , B , M không thẳng hàng , ba điểm A , B , N thẳng hàng
a) Chứng tỏ bốn điểm A , B , C và N cùng 1đường thẳng ( giả sử đó là đường thẳng d )
b) Trong cách viết sau , cách nào đùng cách nào sai
A thuộc d
B không thuộc d
M thuộc d
N không thuộc d
c ) Hai đường thẳng AN và BC có là 2 đường thẳng phân biệt không ?
Hai đường thẳng AB và MN có là 2 đường thẳng trùng nhau không ?
d ) Có bao nhiêu đường thẳng đi qua từng cặp 2 điểm trong số 5 điểm đã cho ?
Chú ý
+ Hai đường thẳng phân biệt hoặc có 1 điểm chung , hoặc không có điểm chung nào
+ Với 2 đường thẳng bất kì thì giữa chúng hoặc có 1 điểm chung ( 2 đường thẳng cắt nhau ) , hoặc không có điểm chung nào ( hai đường thẳng song song ) , hoặc có vô số điểm chung ( Hai đường thẳng trùng nhau ).
cho hàm số y=x2 có đồ thị là parabol (P) và hàm số y=x+2 có đồ thị là đường thảng d
a) cmr: (P) luôn cắt (d) tại hai điểm phân biệt A,B. tìm tọa độ 2 điểm đó
b) xác định M có hoành độ dương trên (P) sao cho M cách đều 2 điểm A và B
GIÚP MÌNH VỚI Ạ
a/ Phương trình hoành độ giao điểm y=x^2 và y=x+2
=>x^2=x+2
<=>x^2-x-2=0
denta=1-4*(-2)=9
x1=2=>y=4(2;4)
x2=-1=>y=1(-1;1)
M(0,5;2,5)
Đúng 0
Bình luận (0)
Cho các phát biểu sau, số phát biểu đúng: 1. Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt 2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt 3. Nếu 1 đường thẳng có 1 điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó 4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng 5. Tồn tại 4 điểm cùng thuộc một mặt phẳng 6. Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng sẽ còn 1 điểm chung khác 7. Trên mỗi mặt phẳng, các kết quả đã biết tr...
Đọc tiếp
Cho các phát biểu sau, số phát biểu đúng:
1. Có một và chỉ một đường thẳng đi qua 2 điểm phân biệt
2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt
3. Nếu 1 đường thẳng có 1 điểm thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó
4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng
5. Tồn tại 4 điểm cùng thuộc một mặt phẳng
6. Nếu 2 mặt phẳng phân biệt có 1 điểm chung thì chúng sẽ còn 1 điểm chung khác
7. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng có thể không đúng
A. 3
B. 4
C. 5
D. 6
Đáp án B
Các phát biểu đúng: 1; 4; 5; 6
2. Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt không thẳng hàng
3. Nếu 1 đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó
7. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng
Đúng 0
Bình luận (0)
Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C):
y
x
+
2
x
-
1
sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB. A. B. C. D.
Đọc tiếp
Có hai điểm A, B phân biệt thuộc đồ thị hàm số (C): y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A.![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án A
Gọi ![]() với
với ![]()
Do A, B đối xứng nhau qua điểm M(3;3) nên M là trung điểm của AB.
Tính được: ![]()
Đúng 0
Bình luận (0)
Có hai điểm A, B phân biệt thuộc đồ thị hàm số
C
:
y
x
+
2
x
-
1
sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB. A.
A
B
2
2
B.
A
B
5
2
C. ...
Đọc tiếp
Có hai điểm A, B phân biệt thuộc đồ thị hàm số C : y = x + 2 x - 1 sao cho A và B đối xứng với nhau qua điểm M(3;3). Tính độ dài đoạn thẳng AB.
A. A B = 2 2
B. A B = 5 2
C. A B = 6 2
D. A B = 3 2
cho hàm số y=x2 có đồ thị là parabol (P) và hàm số y=x+2 có đồ thị là đường thảng d
a) cmr: (P) luôn cắt (d) tại hai điểm phân biệt A,B. tìm tọa độ 2 điểm đó
b) xác định M có hoành độ dương trên (P) sao cho M cách đều 2 điểm A và B
Cho góc xOy bằng 100 độ, điểm H thuộc tia phân giác của góc đó. Đường vuông góc với OH tại h cắt các tia Ox, Oy theo thứ tự ở A và B
a, CMR: HA=HB ; OA = OB
b, Trên nửa mặt phẳng không chứa O bờ AB, vẽ tam giác đều ABC. CMR ba điểm O, H, C thẳng hàng
Ta có OH\(\perp\)AB
=>OH là đường cao
Mà HC là đường cao của ∆OAB
=>∆OAB là ∆ cân
=> Oh cũng là đường trung trực của AB
=> HA=HB (1)
Xét ∆OAB có: OA=OB (2)
Từ (1) và (2) =>HA=HB; OA=OB(đpcm)
b, Ta có HA=HB(cmt)
=>HC là trung tuyến của ∆ABC
Mà ∆ ABC là ∆ đều
=>HC là đường trung trực của AB(2)
Từ (1);(2)=> O;H;C thẳng hàng (đpcm)
Đúng 0
Bình luận (0)














