Cho\(\Delta\)ABC cân tại A có AC cố định. Tìm quỹ tích trung điểm BC

Những câu hỏi liên quan
Cho đoạn thẳng BC cố định. Lấy điểm A bất kì sao cho tam giác ABC cân tại A. Tìm quỹ tích điểm A?
A. Đường tròn tâm B bán kính BC.
B. Đường tròn tâm C bán kính BC.
C. Đường trung trực của đoạn thẳng BC.
D. Đường tròn đường kính BC.
Chọn đáp án C.
Do tam giác ABC cân tại A nên AB = AC
Suy ra, A thuộc đường trung trực của đoạn thẳng BC.
Đúng 0
Bình luận (0)
Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại A.Gọi M và N lần lượt là trung điểm BC và AC. Tìm quỹ tích điểm N . A. Đường tròn đường kính MC B. Đường tròn đường kính BC C. Đường tròn đường kính BM. D. Đáp án khác
Đọc tiếp
Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại A.
Gọi M và N lần lượt là trung điểm BC và AC. Tìm quỹ tích điểm N .
A. Đường tròn đường kính MC
B. Đường tròn đường kính BC
C. Đường tròn đường kính BM.
D. Đáp án khác
Chọn đáp án A.
Xét tam giác ABC có M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác ABC.
S u y r a : M N / / A B L ạ i c ó : A B ⊥ A C ⇒ M N ⊥ A C
Suy ra: 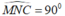
Vì B và C cố định nên trung điểm M của BC cũng cố định
Do đó, quỹ tích các điểm N là đường tròn đường kính MC.
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) có M là điểm di động trên cạnh BC, I là trung điểm AM.
a) Xác định quỹ tích điểm I
b) Qua M, kẻ đường thẳng song song AB cắt AC tại E và đường thẳng song song AC cắt AB tại F. Trung điểm đoạn EF di chuyển trên đường nào?
Bài 1 Cho tam giác ABC vuông tại A, BC cố địnha) Tìm quỹ tích điểm Ab) Gọi P là tđ AC. Tìm quỹ tích điểm P Nghe bảo quỹ tích của lớp 9Nhg cô mình dạy r:((Mn giúp mình với
Cho hai điểm B và C cố định. Lấy A là điểm bất kì sao cho tam giác ABC cân tại A. Gọi H là trực tâm của tam giác ABC. Tìm quỹ tích điểm H
A. Đường tròn đường kính BC
B. Đường trung trực của đoạn thẳng BC
C. Đường tròn tâm B, bán kính BC
D. Đường tròn tâm C, bán kính BC
Chọn đáp án B.
Vì H là trực tâm của tam giác ABC nên A H ⊥ B C
Lại có tam giác ABC là tam giác cân tại A nên đường cao AH đồng thời là đường trung trực.
Suy ra: H nằm trên đường trung trực của đoạn thẳng BC.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm 1 khi điểm A thay đổi
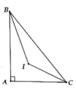
Tương tự câu 1
Tính được B I C ^ = 135 0
=> Quỹ tích của điểm I là hai cung chứa góc 135 0 dựng trên đoạn BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A .M là trung điểm của BC và I là trung điểm của AC .Chứng minh rằng AM cố định ,B và C di động trên đường thẳng vuông góc với AM sao cho tam giác ABC cân tại A thì sẽ di động trên một đường thẳng cố định
Cho \(\Delta ABC\)cân tại A. Một điểm P di động trên BC. Qua P vẽ PQ//AC (\(Q\in AB\)) và PR//AB (\(R\in AC\)). Tìm quỹ tích các điểm D đối xứng với P qua QR.
Cho tam giác ABC có hai đỉnh B, C cố định BC 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là A. Đường thẳng x+2y+4a0 D. Parabôn y2ax2
Đọc tiếp
Cho tam giác ABC có hai đỉnh B, C cố định BC = 2a và đỉnh A thay đổi. Qua B dựng đường thẳng d vuông góc với BC, d cắt đường trung tuyến AI của tam giác ABC tại K. Gọi H là trực tâm của tam giác ABC, biết rằng IH song song với KC. Tìm quỹ tích điểm A là
A. Đường thẳng x+2y+4a=0
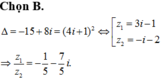
![]()
D. Parabôn y=2ax2










