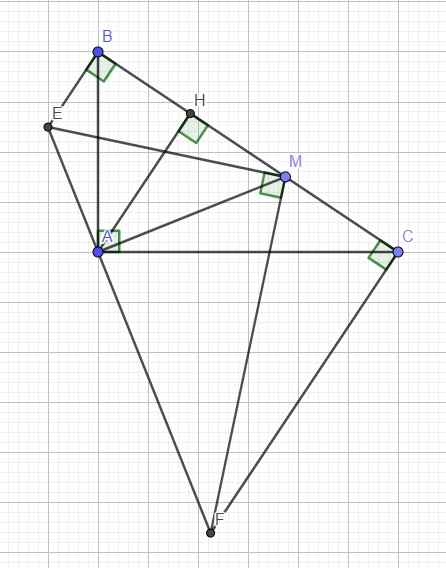
Cho tam giác ABC vuông tại A( số đo góc ABC lớn hơn \(60^0\)), lấy điểm M trên cạnh BC. Trên nửa mặt phẳng bờ BC có chứa điểm A, kẻ các tia Bx và Cy cùng vuông góc với BC. Qua A kẻ đường thẳng vuông góc với AM, cắt Bx tại E và cắt Cy tại F.
a) Chứng minh tam giác CAM đồng dạng với tam giác BAD
b) Chứng minh tam giác ABC đồng dạng với tam giác ADM
c) Chứng minh \(\dfrac{AE}{AC}=\dfrac{AM}{AB}\) và \(MD^2=DA.DE\)
d)Tìm vị trí của điểm M trên cạnh BC để \(S_{\Delta ABC}=\dfrac{1}{4}S_{\Delta MDE}\)