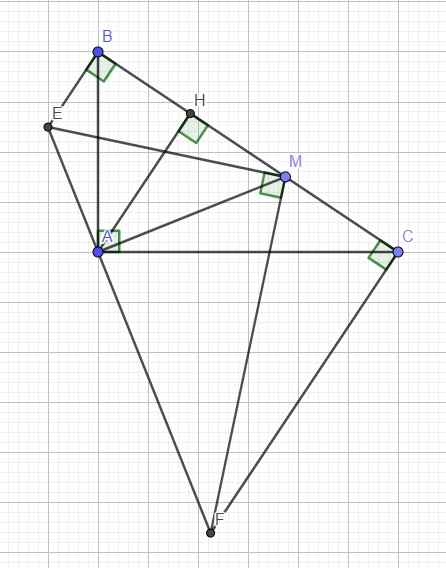
1. Cho ΔABC vuông tại A. Trên cùng một nửa mặt phẳng chứa điểm A có bờ là đường thẳng BC kẻ các tia Bx, Cy cùng vuông góc với BC. Đường thẳng qua A vuông góc với AM ( M thuộc đoạn BC ) cắt Bx tại E và Cy tại F.
Chứng minh rằng:
a) ΔAFC đồng dạng với ΔAMB.
b) ΔFME là tam giác vuông.
c) Tìm vị trí điểm M trên cạnh BC để diện tích ΔMEF đạt min?
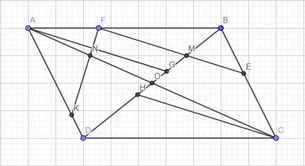
2. Cho hình bình hành ABCD có ^A < 90o, hai đường chéo AC và BD cắt nhau tại O. Gọi N là trung điểm AO; M là trung điểm BO. Trên cạnh AB lấy điểm F sao cho tia FM cắt cạnh BC tại E và tia FN cắt cạnh AD tại K.
Chứng minh rằng:
a) \(\dfrac{BA}{BF}+\dfrac{BC}{BE}=4\)
b) \(BE+AK\) ≥ \(BC\)
1c (2 câu kia em tự giải)
Kẻ đường cao AH \(\Rightarrow\) AH cố định
Do \(\widehat{MAF}\) và \(\widehat{MCF}\) cùng nhìn MF dưới 1 góc vuông nên tứ giác MAFC nội tiếp
\(\Rightarrow\widehat{AFM}=\widehat{ACM}\) (cùng chắn AM)
\(\Rightarrow\Delta_VFME\sim\Delta_VCAB\left(g.g\right)\) với tỉ số đồng dạng \(k=\dfrac{AM}{AH}\)
\(\Rightarrow S_{MEF}=k^2.S_{ABC}\Rightarrow S_{MEF-min}\) khi \(k_{min}\)
Mà trong tam giác vuông AHM ta có \(AH\le AM\Rightarrow k\ge1\Rightarrow k_{min}=1\) khi M trùng H
Hay diện tích MEF min khi M là chân đường cao từ A xuống BC
2.
Kẻ AG, CH song song EF (G, H cùng thuộc BD)
\(\widehat{OAG}=\widehat{OCH}\left(slt\right)\) ; OA=CO; \(\widehat{AOG}=\widehat{COH}\left(đđ\right)\Rightarrow\Delta AOG=\Delta COH\)
\(\Rightarrow OG=OH\)
Theo Talet:
\(\dfrac{BA}{BF}=\dfrac{BG}{BM}\) ; \(\dfrac{BC}{BE}=\dfrac{BH}{BM}\)
\(\Rightarrow\dfrac{BA}{BF}+\dfrac{BC}{BE}=\dfrac{BG+BH}{BM}=\dfrac{\left(BO-OG\right)+\left(BO+OH\right)}{BM}=\dfrac{2BO}{BM}=4\)
b.
Tương tự câu a, ta có: \(\dfrac{BA}{AF}+\dfrac{DA}{AK}=4\Rightarrow\dfrac{BA}{AF}+\dfrac{BC}{AK}=4\)
\(\Rightarrow8=BA\left(\dfrac{1}{BF}+\dfrac{1}{AF}\right)+BC\left(\dfrac{1}{BE}+\dfrac{1}{AK}\right)\ge\dfrac{4BA}{BF+AF}+\dfrac{4BC}{BE+AK}\)
\(\Rightarrow8\ge4+\dfrac{4BC}{BE+AK}\Rightarrow\dfrac{BC}{BE+AK}\le1\)
\(\Rightarrow BE+AK\ge BC\)
Dấu "=" xảy ra khi F là trung điểm AB
Tứ giác AEBM nội tiếp \(\Rightarrow\widehat{AME}=\widehat{ABE}\)
Tứ giác AFCM nội tiếp \(\Rightarrow\widehat{AMF}=\widehat{ACF}\)
Mà \(\widehat{ABF}+\widehat{ACF}=90^0-\widehat{ABC}+90^0-\widehat{ACB}=90^0\)
\(\Rightarrow\widehat{AME}+\widehat{AMF}=90^0\)