
Giải giúp bài 12;14;15 vs ạ
Thank you😙😙😍
Giải giúp mik bài 12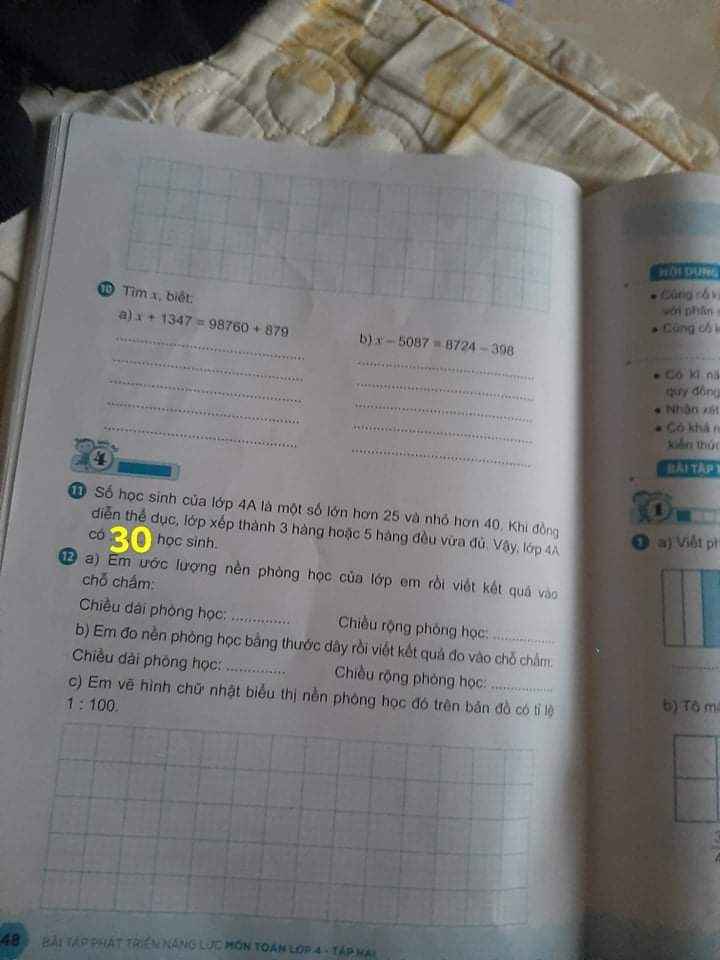
 giải giúp em bài 11 12 13 của bài 14 đi ạ
giải giúp em bài 11 12 13 của bài 14 đi ạ
11.
\(=\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{x-9}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}-2}{3+\sqrt{x}}\)
12.
\(=\frac{(3-\sqrt{x})(3\sqrt{x}-2)+(5\sqrt{x}+7)(3\sqrt{x}+4)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+52\sqrt{x}+22}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+10\sqrt{x}-12}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(3\sqrt{x}-2)(2\sqrt{x}+3)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(2\sqrt{x}+3)}{5\sqrt{x}+7}\)
13.
\(=\frac{(\sqrt{x}+2)(2\sqrt{x}-3)+(3\sqrt{x}-4)(-\sqrt{x}+2)}{(-\sqrt{x}+2)(2\sqrt{x}-3)}+\frac{-7\sqrt{x}+10}{(-\sqrt{x}+2)(2\sqrt{x}-3)}\)
\(=\frac{-x+11\sqrt{x}-14}{(-\sqrt{x}+2)(2\sqrt{x}-3)}+\frac{-7\sqrt{x}+10}{(-\sqrt{x}+2)(2\sqrt{x}-3)}\)
\(=\frac{-x+4\sqrt{x}-4}{(-\sqrt{x}+2)(2\sqrt{x}-3)}=\frac{-(\sqrt{x}-2)^2}{-(\sqrt{x}-2)(2\sqrt{x}-3)}=\frac{\sqrt{x}-2}{2\sqrt{x}-3}\)
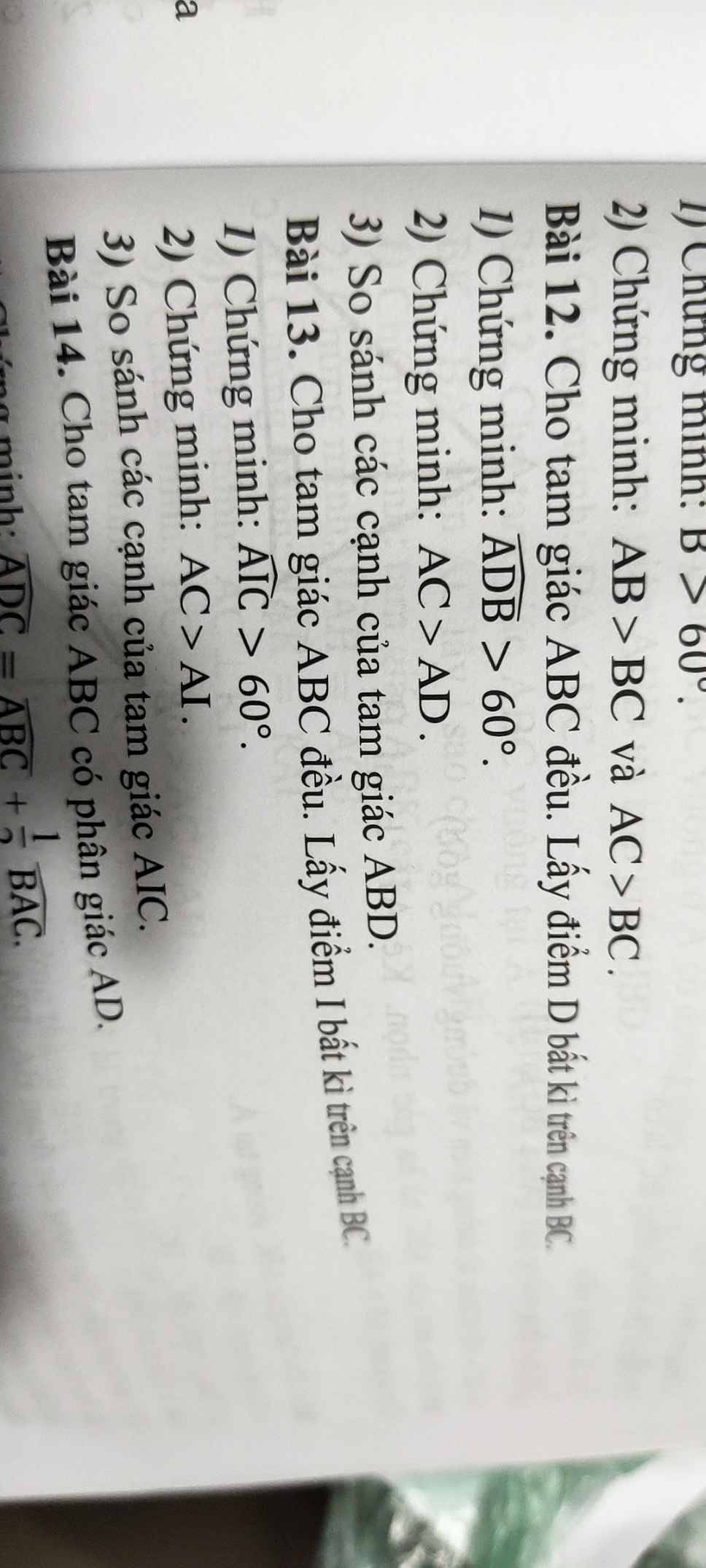
Mấy bạn học giỏi ơi, giải giúp m bài 13, bài 12 đi mà
Bài 13:
a: Xét ΔAIB có \(\widehat{AIC}\) là góc ngoài tại đỉnh I
nên \(\widehat{AIC}=\widehat{ABI}+\widehat{BAI}=60^0+\widehat{BAI}\)
=>\(\widehat{AIC}>60^0\)
b: Ta có: \(\widehat{AIC}>60^0\)
\(\widehat{ACI}=60^0\)
Do đó: \(\widehat{AIC}>\widehat{ACI}\)
Xét ΔAIC có \(\widehat{AIC}>\widehat{ACI}\)
mà AC,AI lần lượt là các cạnh đối diện của các góc AIC và ACI
nên AC>AI
3: Vì I nằm giữa B và C nên tia AI nằm giữa hai tia AB và AC
=>\(\widehat{BAI}+\widehat{CAI}=\widehat{BAC}\)
=>\(\widehat{BAI}+\widehat{CAI}=60^0\)
=>\(\widehat{CAI}< 60^0\)
=>\(\widehat{CAI}< \widehat{ACI}< \widehat{AIC}\)
Xét ΔACI có \(\widehat{CAI}< \widehat{ACI}< \widehat{AIC}\)
mà CI,AI,AC lần lượt là các cạnh đối diện của các góc CAI;ACI;AIC
nên CI<AI<AC
Bài 12:
a: Xét ΔADC có \(\widehat{ADB}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADB}=\widehat{DAC}+\widehat{ACD}\)
=>\(\widehat{ADB}=60^0+\widehat{DAC}\)
=>\(\widehat{ADB}>60^0\)
b: Xét ΔADB có \(\widehat{ADB}>\widehat{ABD}\)
mà AB,AD là các cạnh đối diện của các góc ADB,ABD
nên AB>AD
mà AB=AC
nên AC>AD
3: Vì D nằm giữa B và C nên tia AD nằm giữa hai tia AB và AC
=>\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)
=>\(\widehat{BAD}+\widehat{CAD}=60^0\)
=>\(\widehat{BAD}< 60^0\)
=>\(\widehat{BAD}< \widehat{ABD}< \widehat{ADB}\)
Xét ΔBAD có \(\widehat{BAD}< \widehat{ABD}< \widehat{ADB}\)
mà BD,AD,AB là các cạnh đối diện của các góc BAD;ABD;ADB
nên BD<AD<AB
giải giúp bài 12 tìm x với ạ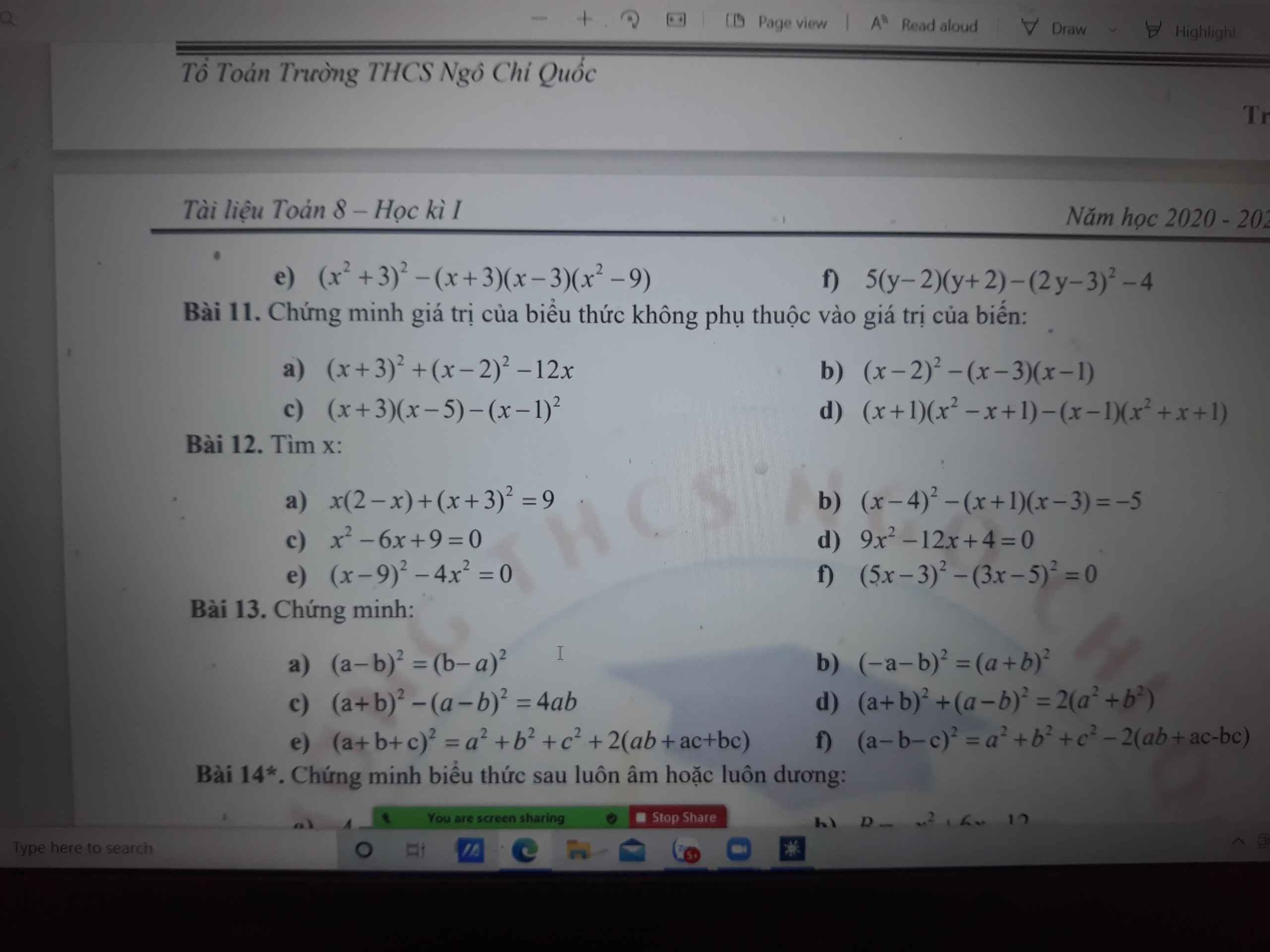
a) \(x\left(2-x\right)+\left(x+3\right)^2=9\)
\(\Leftrightarrow-x^2+2x+x^2+6x+9=9\)
\(\Leftrightarrow8x=0\Leftrightarrow x=0\)
b) \(\Leftrightarrow x^2-8x+16-x^2+2x+3=-5\)
\(\Leftrightarrow-6x=-24\Leftrightarrow x=4\)
c) \(\Leftrightarrow\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\Leftrightarrow x=3\)
d) \(\Leftrightarrow\left(3x-2\right)^2=0\)
\(\Leftrightarrow3x-2=0\Leftrightarrow x=\dfrac{2}{3}\)
e) \(\Leftrightarrow\left(x-9-2x\right)\left(x-9+2x\right)=0\)
\(\Leftrightarrow-3\left(x+9\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=3\end{matrix}\right.\)
f) \(\Leftrightarrow\left(5x-3-3x+5\right)\left(5x-3+3x-5\right)=0\)
\(\Leftrightarrow16\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
giải giúp mình bài này với
\(\sqrt{12+6\sqrt{3}}+\sqrt{12-6\sqrt{3}}\)
Ta có :
A=\(\sqrt{12+6\sqrt{3}}+\sqrt{12-6\sqrt{3}}\)
=\(\sqrt{9+6\sqrt{3}+3}+\sqrt{9-6\sqrt{3+3}}\)
=\(\sqrt{3^2+2.3.\sqrt{3}+\left(\sqrt{3}\right)^2}-\sqrt{3^2-2.3\sqrt{3}+\left(\sqrt{3}\right)^2}\)
=\(\sqrt{\left(3+\sqrt{3}\right)^2}+\sqrt{\left(3-\sqrt{3}\right)^2}\)
=\(3+\sqrt{3}+3-\sqrt{3}=6\)
Vậy A =6
Giải giúp mình với ạ nó liên quan tới bài 12 với bài 15 luôn ạ
Bài 1 chứng minh rằng các số sau ko phải là số chính phương
a)12^12+13^12+14^12
b)7^100+161
các bạn trình bày bài giải ra giúp mình nhé
 Giải giúp câu 10 11 12 13 của bài 15 i
Giải giúp câu 10 11 12 13 của bài 15 i
`11)1/(3+sqrt5)+1/(sqrt5-3)=(3-sqrt5)/(9-5)+(sqrt5+3)/(5-9)=(3-sqrt5-3-sqrt5)/4=-sqrt5/2` $\\$ `12)1/(sqrt2-sqrt6)-1/(sqrt6-sqrt2)=(sqrt2+sqrt6)/(2-6)-(sqrt6-sqrt2)/(6-2)=(-sqrt2-sqrt6-sqrt6+sqrt2)/4=-sqrt6/2` $\\$ `13)1/(sqrt2-sqrt3)-3/(sqrt{18}+2sqrt3)=(sqrt2+sqrt3)/(2-3)-(3(sqrt{18}-2sqrt3))/(18-12)=-(sqrt2+sqrt3)-(sqrt{18}-3sqrt2)/2=(-2sqrt2-2sqrt3-3sqrt2+2sqrt3)/2=-(5sqrt2)/2` $\\$ `14)3/(1-sqrt2)+(sqrt2-1)/(sqrt2+1)=(3(1+sqrt2))/(1-2)+(sqrt2-1)^2/(2-1)=-3(1+sqrt2)+3-2sqrt2=-5sqrt2`
Mình đọc không kĩ xin lỗi bạn.
`10)(sqrt5+sqrt6)/(sqrt5-sqrt6)+(sqrt6-sqrt5)/(sqrt6+sqrt5)`
`=(sqrt5+sqrt6)^2/(5-6)+(sqrt6-sqrt5)^2/(6-5)`
`=((sqrt6-sqrt5)^2-(sqrt6+sqrt5)^2)/1`
`=11-2sqrt{30}-11-2sqrt{30}=-4sqrt{30}`
Các bạn giúp mik giải bài 12 và 13 vs ạ
Bài 12:
a)Có \(H\left(-x\right)=\dfrac{1}{2}\left[f\left(-x\right)+f\left[-\left(-x\right)\right]\right]=\dfrac{1}{2}\left[f\left(-x\right)+f\left(x\right)\right]=H\left(x\right)\)
=>Hàm \(H\left(x\right)\) là hàm chẵn xác định trên S
b)\(G\left(-x\right)=\dfrac{1}{2}\left[f\left(-x\right)-f\left(-\left(-x\right)\right)\right]=\dfrac{1}{2}\left[f\left(-x\right)-f\left(x\right)\right]=-G\left(x\right)\)
=>Hàm \(G\left(x\right)\) là hàm chẵn xác định trên S
Bài 13:
Giải sử pt \(f\left(x\right)=g\left(x\right)\) có nghiệm là a
\(\Rightarrow f\left(a\right)=g\left(a\right)\)
Vì f(x) tăng trên R hay f(x) đồng biến, g(x) giảm trên R hay g(x) là nghịch biến
Tại \(x>a\Rightarrow f\left(x\right)>f\left(a\right)=g\left(a\right)>g\left(x\right)\)
Tại \(x< a\Rightarrow f\left(x\right)< f\left(a\right)=g\left(a\right)< g\left(x\right)\)
\(\Rightarrow\)Với \(x>a;x< a\) thì \(f\left(x\right)=g\left(x\right)\) vô nghiệm
Vậy \(f\left(x\right)=g\left(x\right)\) chỉ có nhiều nhất một nghiệm.
Tính: -12 . 65 + 7 . 12 - 8 . (-12)
CÁC BẠN GIẢI CHI TIẾT BÀI NÀY GIÚP MÌNH NHÉ! CẢM ƠN CÁC BẠN RẤT NHIỀU! 🤧🙏💖
\(\left(-12\right).65+7.12-8.\left(-12\right)\)
\(=-12\left(65-7-8\right)\)
\(=-12.50\)
\(=-600\)