đồ thị hàm số x=0 là như nào neeu ddingj nghĩa . Lấy ví dụ!

Những câu hỏi liên quan
* Đồ thị hàm số, hàm số, đồ thị. Mấy cái này khác nhau như thế nào vậy ạ? Lấy ví dụ giúp mình nhá! *Tìm tọa độ giao điểm của 2 đồ thị + Tọa độ giao điểm của 2 đồ thị nghĩa là như nào ạ?+ Nếu làm theo cách vẽ đồ thị thì đối với trường hợp nào. Và cách giải theo vẽ đồ thị hàm số như nào ạ? + Với nhiều hàm số trở lên thì làm như nào ạ? + Hoành độ giao điểm của 2 đồ thị là nghiệm của phương trình. Tại sao là hoành độ giao điểm mà không phải tung độ giao điểm ạ? + Ví dụ y -2x+3 (d1). Mình gọi (d1)...
Đọc tiếp
* Đồ thị hàm số, hàm số, đồ thị. Mấy cái này khác nhau như thế nào vậy ạ? Lấy ví dụ giúp mình nhá!
*Tìm tọa độ giao điểm của 2 đồ thị
+ Tọa độ giao điểm của 2 đồ thị nghĩa là như nào ạ?
+ Nếu làm theo cách vẽ đồ thị thì đối với trường hợp nào. Và cách giải theo vẽ đồ thị hàm số như nào ạ?
+ Với nhiều hàm số trở lên thì làm như nào ạ?
+ Hoành độ giao điểm của 2 đồ thị là nghiệm của phương trình. Tại sao là hoành độ giao điểm mà không phải tung độ giao điểm ạ?
+ Ví dụ y= -2x+3 (d1). Mình gọi (d1) là đường thẳng. Đường thẳng này khác với hàm số như nào ạ. Ví dụ thay x = 2 vào (d1) thì không đung mà phải nói thay x = 2 vào y = -2x+3 thì mới đúng ạ? Mà mình đặt hàm số đó là đường thẳng (d1) vậy tại sao khác nhau như nào ạ?
Lời giải:
Nói đơn giản thế này. Khi đề cho: Cho đồ thị hàm số $y=x+2$
- Hàm số: chính là $y=x+2$, biểu diễn mối quan hệ giữa biến $x$ và biến $y$. Hàm số hiểu đơn giản giống như phép biểu diễn mối quan hệ giữa hai biến.
- Đồ thị hàm số (hay đồ thị): Khi có hàm số rồi, người ta muốn biểu diễn nó trên mặt phẳng tọa độ ra được 1 hình thù nào đó thì đó là đồ thị hàm số. Ví dụ, đths $y=x+2$ có dạng như thế này:
Đúng 1
Bình luận (0)
- Tọa độ giao điểm của hai đồ thị: Khi ta vẽ được đồ thị trên mặt phẳng tọa độ, 2 đồ thị đó giao nhau ở vị trí nào thì đó chính là tọa độ giao điểm. Ví dụ, trên mp tọa độ ta có 2 đồ thị $y=-2x+3$ và $y=x+6$ chả hạn. Điểm $A$, có tọa độ $(-1,5)$ chính là giao điểm. Như vậy, $(-1,5)$ là tọa độ giao điểm.
- Nhìn hình vẽ của đồ thị chỉ giúp ta có cái nhìn trực quan hơn. Khi muốn tìm giao điểm của 2 đồ thị hàm số, người ta thường dùng hàm số để tìm cho nhanh, vì hàm số biểu diễn mối quan hệ giữa hai biến một cách "số hóa" hơn.
- Với nhiều hàm số trở lên thì ta cứ xét từng cặp 1 thôi.
Đúng 1
Bình luận (2)
- Tung độ giao điểm cũng được, nhưng không hay dùng. Vì sao? Vì khi biểu diễn đồ thị hàm số, người ta hay biểu diễn $y=ax+b$. Lấy ví dụ, có 2 đths có phương trình $y=-2x+3$ và $y=x+6$ chả hạn. Người ta muốn tìm giao điểm $A(x_A,y_A)$
Vì $A$ thuộc 2 đths nên:
$y_A=-2x_A+3$
$y_A=x_A+6$
Tức là: $y_A=-2x_A+3=x_A+6$
Rút gọn lại: $-2x_A+3=x_A+6$ (chỉ còn hoành độ )
Nhưng người ta không muốn đặt $x_A$ làm gì cho mất thời gian. Vì vậy, người ta nói luôn, pt hoành độ giao điểm:
$-2x+3=x+6$. Giải được $x$ ta tìm được hoành độ giao điểm.
---------------------------------
Về câu ví dụ:
$(d_1)$ là hình vẽ được biểu diễn trên mặt phẳng tọa độ, còn hàm số $y=-2x+3$ là 1 hàm số biểu diễn mối quan hệ giữa $x$ và $y$. Như vậy, 1 cái là hình, 1 cái là hàm số liên quan đến biến, số thì đương nhiên khác nhau.
Hình vẽ thì không thể thay số được là đương nhiên, mà ta phải thay số vào biểu thức/ hàm số chứ. Cái này ta đã được học từ lớp 7 rồi.
Em còn chỗ nào chưa hiểu không?
Đúng 1
Bình luận (2)
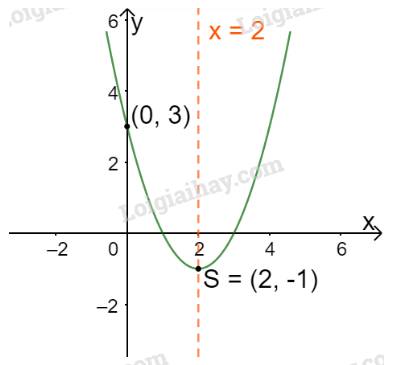
Vẽ đồ thị hàm số \(y = {x^2} - 4x + 3\) rồi so sánh đồ thị hàm số này với đồ thị hàm số trong Ví dụ 2z. Nếu nhận xét về hai đồ thị này.
Tham khảo:
Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\) là một parabol (P1):
+ Có đỉnh S với hoành độ: \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - ( - 4)}}{{2.1}} = 2;{y_S} = {2^2} - 4.2 + 3 = - 1.\)
+ Có trục đối xứng là đường thẳng \(x = 2\) (đường thẳng này đi qua đỉnh S và song song với trục Oy);
+ Bề lõm quay lên trên vì \(a = 1 > 0\)
+ Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).
Ta vẽ được đồ thị như hình dưới.
*So sánh với đồ thị hàm số ở Ví dụ 2a:
Giống nhau: Có chung trục đối xứng
Khác nhau:
Điểm đỉnh và giao điểm với trục tung của hai hàm số đối xứng với nhau qua trục Ox.
Bề lõm của (P) xuống dưới còn (P1) quay lên trên.
Nhận xét chung: Hai đồ thị này đối xứng với nhau qua trục Ox.
Đúng 0
Bình luận (0)
a) Đồ thị hàm số y = ax ( a \(\ne\)0) có dạng như thế nào? cho ví dụ
b) Vẽ đồ thị của hàm số y = ax
c) Điểm nào dưới đây không thuộc đồ thị của hàm số y = \(\frac{2}{3}\)x
A ( -1 ; -2 ) và B ( 3 ; 2)
GIẢI CHI TIẾT LUÔN NHA
PLEASE
CẢM ƠN MỌI NGƯỜI
cho một ví dụ về hàm số bậc nhất với hệ số a dương
1/timg hệ số gốc , tung dộ gốc
2/ vẽ đồ thị hàm số
3/ tìm gốc tạo bởi đồ thị và trục Ox
*lưu ý ko lấy trong sách ,mà tự cho
Các bạn ơi chỉ mình : Ví dụ như trong căn phải là số không âm ví dụ như căn (x-1) thì lúc nào x cũng luôn lớn hơn hoặc bằng 0 rồi nhưng sao phải lấy cả x-1 >=0 ạ
Đề ví dụTimf x không âm biết căn (x-1)=...... Đề bải x không âm thì chỉ cần x>=0 thôi chứ ạ. Chỉ rõ chio mình hiểu nhá
Đúng 0
Bình luận (0)
Vì khi lấy ĐKXĐ thì lấy cả biểu thức trong căn mới đúng
Đúng 0
Bình luận (0)
Các bạn ơi chỉ mình : Ví dụ như trong căn phải là số không âm ví dụ như căn (x-1) thì lúc nào x cũng luôn lớn hơn hoặc bằng 0 rồi nhưng sao phải lấy cả x-1 >=0 ạ
Thì ĐKXĐ là phải lấy tất cả các biểu thức trong căn phải không âm
Đúng 0
Bình luận (0)
Bạn nhớ rằng $\sqrt{a}$ xác định khi mà $a\geq 0$, hay $a$ không âm.
Cho $a=x-1$ thì để $\sqrt{x-1}$ xác định thì $x-1\geq 0$
$\Leftrightarrow x\geq 1$
Đúng 1
Bình luận (0)
Hàm số
y
a
x
4
+
b
x
2
+
c
(
a
≠
0
)
có đồ thị như hình vẽ sau:Hàm số y f(x) là hàm số nào trong bốn hàm số sau:
A
.
y
(
x
2
+
2
)
2
-
1
B...
Đọc tiếp
Hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) có đồ thị như hình vẽ sau:
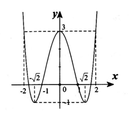
Hàm số y = f(x) là hàm số nào trong bốn hàm số sau:
A . y = ( x 2 + 2 ) 2 - 1
B . y = ( x 2 - 2 ) 2 - 1
C . y = - x 4 + 2 x 2 + 3
D . y = - x 4 + 4 x 2 + 3
Xét hàm số y S(x) - 2{x^2} + 20x(0 x 10)a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số y - 2{x^2} + 20xtrên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị y - 2{x^2} + 20x có giống với đồ thị của hàm số y - 2{x^2} hay không?b) Quan sát dạng đồ thị của hàm số y - 2{x^2} + 20x trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.c) Thực hiện phép biến đổi y - 2{x^2} + 20x ...
Đọc tiếp
Xét hàm số \(y = S(x) = - 2{x^2} + 20x(0 < x < 10)\)
a) Trên mặt phẳng tọa độ Oxy, biểu diễn tọa độ các điểm trong bảng giá trị của hàm số lập được ở Ví dụ 1. Nối các điểm đã vẽ lại ta được dạng đồ thị hàm số \(y = - 2{x^2} + 20x\)trên khoảng (0; 10) như trong Hình 6.10. Dạng đồ thị \(y = - 2{x^2} + 20x\) có giống với đồ thị của hàm số \(y = - 2{x^2}\) hay không?
b) Quan sát dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\) trong Hình 6.10, tìm tọa độ điểm cao nhất của đồ thị.
c) Thực hiện phép biến đổi \(y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\) Hãy cho biết giá trị lớn nhất của diện tích mảnh đất được rào chắn. Từ đó suy ra lời giải của bài toán ở phần mở đầu.
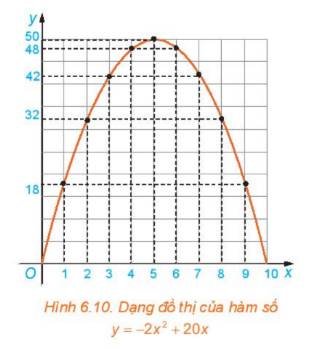
a) Ta có đồ thị hàm số \(y = - 2{x^2}\)
Nhìn vào 2 đồ thị, ta thấy dạng đồ thị của hàm số \(y = - 2{x^2} + 20x\)giống với dạng đồ thị \(y = - 2{x^2}\)
b) Tọa độ điểm cao nhất là \(\left( {5;50} \right)\)
c) Ta có: \(S(x) = y = - 2{x^2} + 20x = - 2({x^2} - 10x) = - 2({x^2} - 2.5.x + 25) + 50 = - 2{(x - 5)^2} + 50\)
\({(x - 5)^2} \ge 0 \Rightarrow - 2{(x - 5)^2} + 50 \le 50 \Rightarrow S(x) \le 50\)
Do đó diện tích lớn nhất của mảnh đất rào chắn là 50 \(({m^2})\) khi x = 5.
Đúng 0
Bình luận (0)
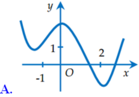
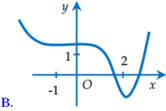
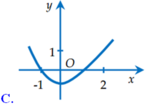
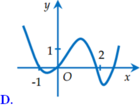
Một trong các đồ thị dưới đây là đồ thị của hàm số g(x) liên tục trên R thỏa mãn g’(0) 0, g’’(x) 0 ∀x ∈ (-1; 2). Hỏi đồ thị của hàm số g(x) là đồ thị nào?
Đọc tiếp
Một trong các đồ thị dưới đây là đồ thị của hàm số g(x) liên tục trên R thỏa mãn g’(0) = 0, g’’(x) < 0 ∀x ∈ (-1; 2). Hỏi đồ thị của hàm số g(x) là đồ thị nào?