hãy tính tỉ số lg giác biết cosα=15/17

Những câu hỏi liên quan
Cho
A
B
C
^
60
0
và ∆ABC tam giác nhọna, Tính sinα, tanα, cotα, biết cosα
1
5
b, Tính cosα, tanα, cotα, biết sinα
2
3
c, Cho tanα 2. Tính sinα, cosα, cotαd, Cho cotα 3. Tính sinα, cosα, tanα
Đọc tiếp
Cho A B C ^ = 60 0 và ∆ABC tam giác nhọn
a, Tính sinα, tanα, cotα, biết cosα = 1 5
b, Tính cosα, tanα, cotα, biết sinα = 2 3
c, Cho tanα = 2. Tính sinα, cosα, cotα
d, Cho cotα = 3. Tính sinα, cosα, tanα
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
Đúng 0
Bình luận (0)
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
a, Sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn: cot
24
0
, tan
16
0
, cot
57
0
, cot
30
0
, tan
80
0
b, Tính cosα, tanα và cotα biết sinα 1/5
Đọc tiếp
a, Sắp xếp các tỉ số lượng giác sau theo thứ tự từ nhỏ đến lớn: cot 24 0 , tan 16 0 , cot 57 0 , cot 30 0 , tan 80 0
b, Tính cosα, tanα và cotα biết sinα =1/5
a, Ta có: cot 24 0 = tan 66 0 ; cot 57 0 = tan 33 0 ; cot 30 0 = tan 60 0
=> tan 16 0 < tan 33 0 < tan 60 0 < tan 66 0 < tan 80 0
=> tan 16 0 < cot 57 0 < cot 30 0 < cot 24 0 < tan 80 0
b, Ta có: cos 2 α = 1 - sin 2 α => cosα = 2 6 5 , tanα = sin α cos α = 6 12 và cotα = cos α sin α = 2 6
Đúng 0
Bình luận (0)
Cho tam giác vuông ABC, biết BC = 17 dm, đường cao AH = 120/17 dm và AB = 15 dm. Hãy tính AC ?
Bài 1: Biết sinα = \(\dfrac{\sqrt{3}}{2}\). Hãy tính cosα, tanα, cotα.
Bài 2: Biết tanα = 2. Hãy tính sinα, cotα, cosα
Bài 3: Tính: A= cos2 20o + cos2 40o + cos2 50o + cos2 70o
Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC vuông tại A
a. Hãy viết các tỉ số lượng giác của góc C
b. Biết AB= 5cm, AC=12cm. Hãy tính các tỉ số lượng giác của góc B
c. Tính B,C (làm tròn đến phút)
\(a,\sin\widehat{C}=\dfrac{AB}{BC};\cos\widehat{C}=\dfrac{AC}{BC};\tan\widehat{C}=\dfrac{AB}{AC};\cot\widehat{C}=\dfrac{AC}{AB}\\ b,BC=\sqrt{AB^2+AC^2}=13\left(cm\right)\left(pytago\right)\\ \Rightarrow\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{12}{13};\cos\widehat{B}=\dfrac{AB}{BC}=\dfrac{5}{13}\\ \tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5};\cot\widehat{B}=\dfrac{AB}{AC}=\dfrac{5}{12}\)
\(\tan\widehat{B}=\dfrac{AC}{AB}=\dfrac{12}{5}\approx\tan67^022'\\ \Rightarrow\widehat{B}\approx67^022'\\ \Rightarrow\widehat{C}=90^0-67^022'=22^038'\)
Đúng 1
Bình luận (0)
Tính các giá trị lượng giác của góc α, biết
cosα = 2sinα khi 0 < α < π/2
Với 0 < α < π/2 thì cosα >0, sinα >0. Ta có
1 - sin 2 α = cos 2 α
Mặt khác cos 2 α = ( 2 sin α ) 2 = 4 sin 2 α nên 5 sin 2 α = 1 hay
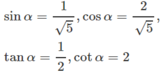
Đúng 0
Bình luận (0)
Bài 1: Biết rằng sinα = 0,6. Tính cosα và tgα.
Bài 2: Biết rằng cosα = 0,7. Tính sinα và tgα.
Bài 3: Biết rằng tgα = 0,8. Tính sinα và cosα.
Bài 4: Biết cosx = \(\dfrac{1}{2}\), tính P = 3sin2x + 4cos2x.
Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
Đúng 1
Bình luận (0)
Cho hai tam giác đồng dạng có tỉ số chu vi là 15/17 và hiệu độ dài hai cạnh tương ứng của chúng là 12,5cm. Tính hai cạnh đó.
Giả sử ΔA’B’C’ 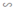 ΔABC có hai cạnh tương ứng là A’B’ và AB có hiệu AB - A'B' = 12,5 (cm)
ΔABC có hai cạnh tương ứng là A’B’ và AB có hiệu AB - A'B' = 12,5 (cm)
ΔA’B’C’ 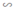 ΔABC ⇒
ΔABC ⇒ 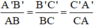
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
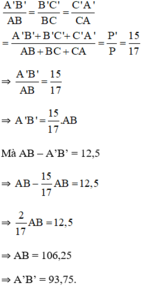
Vậy hai cạnh cần tìm là 106,25 và 93,75.
Đúng 0
Bình luận (0)