Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
Bài 1:
\(\cos\alpha=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
Bài 2:
\(\sin\alpha=\sqrt{1-\dfrac{49}{100}}=\dfrac{\sqrt{51}}{10}\)
\(\tan\alpha=\dfrac{\sqrt{51}}{7}\)
Tìm góc nhọn α , biết sinα = cosα .
Cho góc nhọn α. CMR:
a) sinα< tanα
b) cosα< cotα
tính góc α biết sinα= 4/5
Bài 1: Tính các độ dài x, y trong hình bên: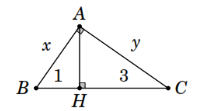
Bài 2: Giải \(\Delta\)ABC vuông tại A, biết AB = 3,5 và AC = 4,2.
Bài 1
Cho tam giác OCD vuông tại O có đường cao OH. Biết CD = 24cm , HC/HD=3/5 . Tính độ dài OH, OC, OD.
Bài 2
Cho tam giác DEF vuông tại D, đường cao DI. Biết DF/EF=4/5 , DE = 18 cm . Giải tam giác DEF và tính độ dài DI.
Bài 1. Giải tam giác vuông ABC, biết: BC = 10cm, góc C = 55 độ.
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 5cm, AC = 12cm.
a) Tính AH.
b) Gọi M, N là hình chiếu của H trên AB, AC. Chứng minh rằng: MN2 = AM.AB.
c) Gọi K là điểm đối xứng của H qua AC. Tính diện tích tứ giác AHCK.
Bài 5. ChoΔ ABC đường cao BM và CN cắt nhau tại H .
a) Biết MA=6 cm;AB=10 cm. Tính các tỉ số lượng giác của góc A.
b) Chứng tỏ rằng góc ABM= góc ACN;AH vuông góc BC .
c) Gọi I ,J lần lượt là trung điểm của AH,BC . Chứng tỏ rằng IJ vuông góc MN .
Bài 5. ChoΔ ABC đường cao BM và CN cắt nhau tại H .
a) Biết MA=6 cm;AB=10 cm. Tính các tỉ số lượng giác của góc A.
b) Chứng tỏ rằng góc ABM= góc ACN;AH vuông góc BC .
c) Gọi I ,J lần lượt là trung điểm của AH,BC . Chứng tỏ rằng IJ vuông góc MN .
Bài tập 3: Cho tam giác MNP vuông tại M, đường cao MH (H thuộc NP). Biết MN = 10cm,
NH = 7cm. Tính NP, MP và SinHMP