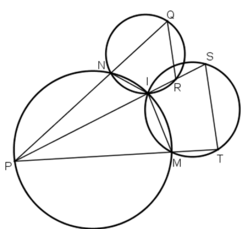
Xem hình 48. Chứng minh QR // ST.

Những câu hỏi liên quan
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong PST ^ , SRQ ^
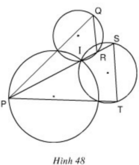
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong P S T ^ , S R Q ^
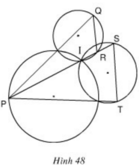
Cho tam giác PQR vuông tại P. Vẽ tia phân giác PS của góc QPR ( S thuộc QR ), vẽ tia PT vuông góc với QR ( T thuộc QR ). Chứng minh rằng góc TPS = 1/2(Q - R).
ko cần vễ hình đâu mọi người.
Mọi người làm hộ mik với nha, mik đag cần gấp.
Với `p;q;r;s\inRR : {(p+q+r+s=0),(p<q<r<s):}` chứng minh rằng: `p<1/2 \root[3]{(\sqrt(24(pq+pr+ps+qr+qs+rs)^3+81(pqr+qrs+rsp+spq)^2)+9(pqr+qrs+rsp+spq))/(9)}-(pq+pr+ps+qr+qs+rs)/(\root[3]{3\sqrt(24(pq+pr+ps+qr+qs+rs)^3+81(pqr+qrs+rsp+spq)^2)+27(pqr+qrs+rsp+spq)})<s`
Nhìn đề đến một người theo Toán như anh còn thấy nản í :)
Đúng 5
Bình luận (4)
ừ thì năm nay lên 11 nma toi đ hiểu đây là cgi =))
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Cho hình vuông ABCD. Qua A kẽ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R, cắt CD tại Q và S.
a) chứng minh tam giác AQR và tam giác APS là hai tam giác cân.
b) QR cắt PS tại H; M, N là trung điểm của QR và PS. Chứng Minh tứ giác AMHN là hình chữ nhật.
c)Chứng minh P là trực tâm của AC.
d) Chứng minh bốn điểm M,B,N,D thẳng hàng
Fuck. Fuck. Fuck. Fuck
Câu 2: cho hình vuông ABCD. Qua A kẻ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R, cắt CD tại Q và S. a, chứng minh tam giác AQR và tam giác APS là tam giác cân.b, QR cắt PS tại H; M,N là trung điểm của QR và PS. chứng minh tứ giác AMHN là hình chữ nhật.c, chứng minh P là trực tâm của tam giác SQRd, MN là đường trung trực của AC.e, chứng minh bốn điểm M,B,N,D thẳng hàng.
Đọc tiếp
Câu 2: cho hình vuông ABCD. Qua A kẻ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R, cắt CD tại Q và S.
a, chứng minh tam giác AQR và tam giác APS là tam giác cân.
b, QR cắt PS tại H; M,N là trung điểm của QR và PS. chứng minh tứ giác AMHN là hình chữ nhật.
c, chứng minh P là trực tâm của tam giác SQR
d, MN là đường trung trực của AC.
e, chứng minh bốn điểm M,B,N,D thẳng hàng.
a) Xét tam giác vuông ABR và ADQ có:
AB = AD (gt)
Góc BAR + góc BAP = 90 độ
Góc DAQ + góc BAP = 90 độ
=> Góc BAR = Góc DAQ
=> Tam giác vuông ABR = tam giác vuông ADQ (cạnh góc vuông – góc nhọn kề)
=> AR = AQ (2 cạnh tương ứng)
=> Tam giác AQR cân tại A.
CMTT ta có tam giác ADS = tam giác ABP
=> AS = AP => Tam giác APS cân tại A.
b) Tam giác AQR cân tại A => Trung tuyến AM đồng thời là đường cao.
=> AM vuông góc với QR => Góc AMH = 90 độ
Tương tự: Tam giác APS cân tại A => Trung tuyến AN đồng thời là đường cao.
=> AN vuông góc với SP => góc ANP = 90 độ hay góc ANH= 90 độ.
Tam giác AQR vuông cân tại A => Góc AQR = góc ARQ = 45 độ => Góc PQH = 45 độ.
Tam giác APS vuông cân tại A => góc ASP = góc APS = 45 độ => góc QPH = 45 độ (đối đỉnh).
Xét tam giác PHQ có: Góc PQH + góc QPH = 45 độ + 45 độ = 90 độ
=> Tam giác PHQ vuông cân tại H => PH vuông góc với PQ
=> góc NHM = 90 độ
Xét tứ giác AMHN có: Góc AMH = góc ANH = góc NHM = 90 độ
=> AMHN là hình chữ nhật (dhnb)
c) Xét tam giác SQR có:
BC vuông góc CD => RC vuông góc SQ => RC là đường cao.
AP vuông góc AR => QA vuông góc RS => QA là đường cao.
Mà RC cắt QA tại P
Vậy P là trực tâm tam giác SQR.
d) Tam giác ANP vuông tại A có trung tuyến AN => AN = SP/2
Tam giác CSP vuông tại C có trung tuyến CN => CN = SP/2
=> AN = CN => N thuộc trung trực của AC.
CMTT ta có MA = MC => M thuộc trung trực của AC.
Vậy MN là trung trực của AC.
e) Ta có BA = BC (gt) => B thuộc trung trực của AC.
Mà MN là trung trực của AC (cmt) => B thuộc MN
Tương tự DA = DC (gt) => D thuộc trung trực của AC.
Mà MN là trung trực của AC (cmt) => D thuộc MN
Vậy M, B, N, D thẳng hàng.
A B C D E x 20 30 40 H1 , DE//BC Q P R S T x 2x+18 5 14 H2, ST//QR 1 Tìm xBài 2.cho tam giác ADE có AD 5cm. Kéo dài AD thêm 1 đoạn DB3cm .từ B vex tia song song với DE cắt AE tại C. biết AE-EC 3cm. tính AE, EC,ACbài 3: cho hình thang ABCD. lấy I trên AD k trên BC sao cho IK // AB .cmr: AI/AD BK/BCbài 4 : Nếu 1 đthẳng ko đi qua các đỉnh của tam giác ABC và cắt các đthẳng BC,CA, AB theo thứ tự A, B, C. cmr: AB/BC . CA/AB .BC/CA 1 giúp mik đi các proooo
Đọc tiếp
1 Tìm x
Bài 2.cho tam giác ADE có AD = 5cm. Kéo dài AD thêm 1 đoạn DB=3cm .từ B vex tia song song với DE cắt AE tại C. biết AE-EC =3cm. tính AE, EC,AC
bài 3: cho hình thang ABCD. lấy I trên AD k trên BC sao cho IK // AB .cmr: AI/AD = BK/BC
bài 4 : Nếu 1 đthẳng ko đi qua các đỉnh của tam giác ABC và cắt các đthẳng BC,CA, AB theo thứ tự A', B', C'. cmr: AB'/B'C . CA'/A'B .BC'/C'A =1
giúp mik đi các proooo
Xem hình dưới và dùng các kí hiệu ∈ hoặc ∉ để điền vào chỗ trống cho thích hợp.
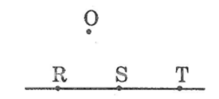
O ... đường thẳng RS
R ... đường thẳng ST
S ... đường thẳng OT
T ... đường thẳng SR
O ∉ đường thẳng RS
R ∈ đường thẳng ST
S ∉ đường thẳng OT
T ∈ đường thẳng SR
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại B ( BC>AB ) . Gọi I là tâm đường tròn nội tiếp tam giác các tiếp điển của đường tròn nội tiếp với các cạnh AB , BC , CA lần lượt là P,Q ,R. a,chứng minh rằng BPIQ là hình vuông b, Đường thẳng PI cắt QR tại D . CHỨNG minh P,A,R,D,I nằm trên 1 đường tròn
Qua đỉnh A của hình vuông ABCD ta kẻ 2 đường thẳng Ax,Ay vuong goc voi nhau.Ax cắt cạnh BC tại điểm P và cắt tia đối của tia CD tại điểm Q .Ay cắt tỉa đối BC tại điểm R và cắt tia đối của tia DC tại điểm S
Chứng minh tam giác APS,AQR là các tam giác cân
Gọi H LÀ GIAO ĐIỂM CỦA QR va PS .M,N là trung điểm của QR và PS Chứng minh tứ giác AMHN là hình chữ nhật




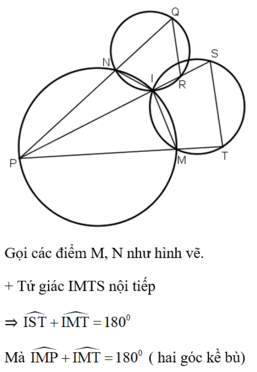


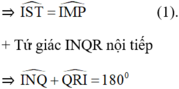 (hai góc kề bù)
(hai góc kề bù)















