Các câu hỏi tương tự
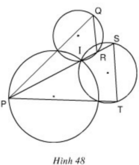
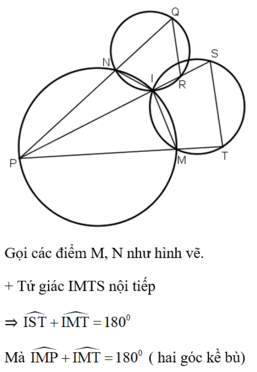
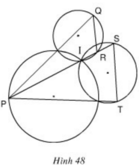
Xem hình 48. Chứng minh QR // ST.
Hướng dẫn: Xét cặp góc so le trong P S T ^ , S R Q ^
Cho hình vuông ABCD. Qua A kẽ hai đường thẳng vuông góc với nhau lần lượt cắt BC tại P và R, cắt CD tại Q và S.
a) chứng minh tam giác AQR và tam giác APS là hai tam giác cân.
b) QR cắt PS tại H; M, N là trung điểm của QR và PS. Chứng Minh tứ giác AMHN là hình chữ nhật.
c)Chứng minh P là trực tâm của AC.
d) Chứng minh bốn điểm M,B,N,D thẳng hàng
Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C chia cung lớn AB thành hai cung AC và CB .chứng minh rằng cung lớn AB có sđ ∠ AB = sđ ∠ AC + sđ ∠ CB
Hướng dẫn: Xét ba trường hợp:
Tia OC nằm trong một góc kề bù với góc ở tâm AOB
Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C chia cung lớn AB thành hai cung AC và CB .chứng minh rằng cung lớn AB có sđ ∠ AB = sđ ∠ AC + sđ ∠ CB
Hướng dẫn: Xét ba trường hợp:
Tia OC nằm trong góc đối đỉnh của góc ở tâm AOB
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
đ
B
n
C
⏜
+
s
đ
A
m...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh: B E C ^ = s đ B n C ⏜ + s đ A m D ⏜ 2
Hãy chứng minh định lý trên.Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B
E
C
^
s
d
B
n
C
^
+
s
d
A
m
D
^...
Đọc tiếp
Hãy chứng minh định lý trên.
Gợi ý: Xem hình 32. Sử dụng góc ngoài của tam giác, chứng minh:
B E C ^ = s d B n C ^ + s d A m D ^ 2
Cho tứ giác ABCD có góc A= Góc C= 90 độ
a) Chứng minh bốn đỉnh của tứ giác cùng thuộc 1 đường tròn
b) Chứng minh AC\(\le\)BD
c) Nếu AC=BD thì tứ giác ABCD là hình gì ?
Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C chia cung lớn AB thành hai cung AC và CB .chứng minh rằng cung lớn AB có sđ
∠
AB sđ
∠
AC + sđ
∠
CBHướng dẫn: Xét ba trường hợp:Tia OC trùng với tia đối của một cạnh của góc ở tâm AOB
Đọc tiếp
Cho C là một điểm nằm trên cung lớn AB của đường tròn (O). Điểm C chia cung lớn AB thành hai cung AC và CB .chứng minh rằng cung lớn AB có sđ ∠ AB = sđ ∠ AC + sđ ∠ CB
Hướng dẫn: Xét ba trường hợp:
Tia OC trùng với tia đối của một cạnh của góc ở tâm AOB
góc so le trong là gì