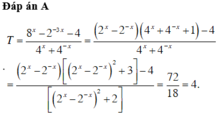giải pt : 0,4+8x / 6,8+44x . 100=14

Những câu hỏi liên quan
Giải pt \(x^4-16x^3+44x^2-12=0\)
\(\Leftrightarrow\left(x^2-12x-6\right)\left(x^2-4x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-12x-6=0\\x^2-4x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left(x-6\right)^2=42\\\left(x-2\right)^2=2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6\in\left\{\sqrt{42};-\sqrt{42}\right\}\\x-2\in\left\{\sqrt{2};-\sqrt{2}\right\}\end{matrix}\right.\Leftrightarrow x\in\left\{\sqrt{42}+6;-\sqrt{42}+6;\sqrt{2}+2;2-\sqrt{2}\right\}\)
Đúng 5
Bình luận (0)
Lên lớp trên mà gửi đi gửi ở lớp 1 làm gì vậy bạn .
Đúng 6
Bình luận (0)
Xem thêm câu trả lời
1.Giải pt:\(2x^2+\left(14-2\sqrt{x^2+8x}\right)x+8x-14\sqrt{x^2+8x}+24=0\)
2. Tìm các số nguyên x, y thoả mãn pt: \(x^2+y^2-xy=x+y+2\)
Kiểm tra lại đề câu a, \(...+24\) thì pt vô nghiệm, phải là \(...-24\) mới có lý
b/ \(x^2-\left(y+1\right)x+y^2-y-2=0\) (1)
\(\Delta=\left(y+1\right)^2-4\left(y^2-y-2\right)\ge0\)
\(\Leftrightarrow-3y^2+6y+9\ge0\)
\(\Leftrightarrow-1\le y\le3\Rightarrow y=\left\{-1;0;1;2;3\right\}\)
Thay lần lượt vào pt ban đầu để tìm x nguyên
ĐKXĐ: ...
\(\Leftrightarrow x^2+\left(x^2+8x\right)+\left(14-2\sqrt{x^2+8x}\right)x-14\sqrt{x^2+8x}+24=0\)
Đặt \(\sqrt{x^2+8x}=a\ge0\) pt trở thành:
\(x^2+a^2+\left(14-2x\right)x-14a+24=0\)
\(\Leftrightarrow x^2-2ax+a^2+14\left(x-a\right)+24=0\)
\(\Leftrightarrow\left(x-a\right)^2+14\left(x-a\right)+24=0\)
\(\Leftrightarrow\left(x-a+2\right)\left(x-a+12\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=x+2\\a=x+12\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+8x}=x+2\left(x\ge-2\right)\\\sqrt{x^2+8x}=x+12\left(x\ge-12\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+8x=x^2+4x+4\\x^2+8x=x^2+24x+144\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=-9\end{matrix}\right.\)
Giải PT: \(\sqrt{3x^2-30x+100}+\sqrt{8x^2-80x+216}=-2x^2+20x-41\)
Biết rằng
2
x
−
2
−
x
4
.
Tính giá trị của biểu thức
T
8
x
−
2
−
3
x
−
4...
Đọc tiếp
Biết rằng 2 x − 2 − x = 4 . Tính giá trị của biểu thức T = 8 x − 2 − 3 x − 4 4 x + 4 − x .
A. T = 4
B. T = 9
C. T = 40 9
D. T = 18
Tim GTNN cua P :
P=\(x^4-8x^3+27x^2-44x+23\)
\(P=x^4-8x^3+24x^2-32x+16+3x^2-12x+12-5\)
\(P=\left(x-2\right)^4+3\left(x-2\right)^2-5\ge-5\)
\(\Rightarrow P_{min}=-5\) khi \(x=2\)
Đúng 0
Bình luận (0)
trả lời :
P=x4 - 8x3 + 27x2 - 44x +23
P= (x-2)4 + 3(x-2)2 - 5 ≥ 5
Pmin= -5 khi x = 2
các bn tham khảo thôi nha (cs khi sai ráng chịu)![]()
Đúng 0
Bình luận (0)
Tim GTNN cua P :
P=\(x^4-8x^3+27x^2-44x+23\)
Lời giải:
Ta có:
\(x^4-8x^3+27x^2-44x+23\)
\(=(x^4-8x^3+16x^2)+11x^2-44x+23\)
\(=(x^2-4x)^2+11(x^2-4x)+23\)
\(=(x^2-4x)^2+8(x^2-4x)+16+3(x^2-4x)+7\)
\(=(x^2-4x+4)^2+3(x^2-4x+4)-5\)
\(=(x-2)^4+3(x-2)^2-5\geq -5\)
Vậy GTNN của $P$ là $-5$ khi $x=2$
Đúng 0
Bình luận (0)
10:25 nhân 6,8 và 0,4 nhân 6,8
10:8 nhân 3,2 và 1,25 nhân 3,2
10:25 x 6,8 và 0,4 x 6,8
10 : 25 x 6,8 = 0,4 x 6,8
= 2,72
0,4 x 6,8 = 2,72
Vậy 10 : 25 x 6,8 = 0,4 x 6,8
10 : 8 x 3,2 và 1,25 x 3,2
10 : 8 x 3,2 = 1,25 x 3,2
= 4
1,25 x 3,2 = 4
Vậy 10 : 8 x 3,2 = 1,25 x 3,2
Đúng 1
Bình luận (0)
Giải PT sau: 1,6x2 \(-\) 2x + 0,4 = 0
=>4x^2-5x+1=0
=>(x-1)(4x-1)=0
=>x=1 hoặc x=1/4
Đúng 0
Bình luận (0)
\(1,6x^2-2x+0,4=0\)
\(\Leftrightarrow\dfrac{8}{5}x^2-2x+\dfrac{2}{5}=0\)
\(\Leftrightarrow\dfrac{8}{5}x^2-\dfrac{8}{5}x-\dfrac{2}{5}x+\dfrac{2}{5}=0\)
\(\Leftrightarrow\dfrac{8}{5}x\left(x-1\right)-\dfrac{2}{5}\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(\dfrac{8}{5}x-\dfrac{2}{5}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\\dfrac{8}{5}x-\dfrac{2}{5}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\dfrac{8}{5}x=\dfrac{2}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{4}\end{matrix}\right.\)
Vậy \(S=\left\{1;\dfrac{1}{4}\right\}\)
Đúng 1
Bình luận (0)
\(1,6x^2-2x+0,4=0\)
\(\Leftrightarrow2,5\left(1,6x^2-2x+0,4\right)=0\)
\(\Leftrightarrow4x^2-5x+1=0\)
\(\Leftrightarrow4x^2-4x-x+1=0\)
\(\Leftrightarrow4x\left(x-1\right)-\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(4x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\4x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(\dfrac{8x^2}{3\left(1-4x^2\right)}=\dfrac{2x}{6x-3}-\dfrac{1+8x}{4+8x}\) giải pt
\(\dfrac{8x^2}{3\left(1-4x^2\right)}=\dfrac{2x}{6x-3}-\dfrac{1+8x}{4+8x}\)
\(\Leftrightarrow\dfrac{8x^2}{3\left(1-2x\right)\left(1+2x\right)}=\dfrac{2x}{3\left(2x-1\right)}-\dfrac{1+8x}{4\left(1+2x\right)}\)
\(\Leftrightarrow\dfrac{-32x^2}{12\left(2x-1\right)\left(2x+1\right)}=\dfrac{2x.4\left(1+2x\right)-\left(1+8x\right).3\left(2x-1\right)}{12\left(2x-1\right)\left(2x+1\right)}\)
\(\Leftrightarrow8x\left(1+2x\right)-\left(1+8x\right).3.\left(2x-1\right)=-32x^2\)
\(\Leftrightarrow8x+16x^2-6x+3-48x^2+24x+32x^2=0\)
\(\Leftrightarrow26x+3=0\)
\(\Leftrightarrow x=-\dfrac{3}{26}\)
Vậy:......
Đúng 1
Bình luận (0)