Cho (E) : \(9x^2+25y^2=225\)
a) Tìm tọa độ hai tiêu điểm \(F_1;F_2\) và các đỉnh của (E)
b) Tìm điểm \(M\in\left(E\right)\) sao cho M nhìn \(F_1F_2\) dưới một góc vuông
Cho elip (E0 có phương trình : \(9x^2+25y^2=225\)
a) Tìm tọa độ các tiêu điểm và các đỉnh của (E)
b) Tìm tọa độ các điểm M thuộc (E) sao cho M nhìn hai tiêu điểm \(F_1\) và \(F_2\) của (E) dưới một góc vuông
Viết lại phương trình (E):\(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\)
a) Từ phương trình ta có: a2=25=>a=5 =>A1(-5;0) A2(5;0)
b2=9=>b=3 =>B1(0;-3) B2(0;3)
c2=a2-b2=25-9=16 =>c=4
=> F1(-4;0) F2(4;0)
b) Giả sử tọa độ điểm M(m;n)
MF1 góc với MF2 => (m+4)(m-4) + n2=0
<=> m2+n2=16 =>9m2+9n2=144(1)
Do M thuộc (E) nên 9m2+25n2=225(2)
Trừ vế với vế của (2) cho (1) ta được 16n2=81
=> \(n=_-^+\dfrac{9}{4}\)
với n\(=\dfrac{9}{4}\)=> m=\(\dfrac{5\sqrt{7}}{4}\)
với n\(=-\dfrac{9}{4}\)=> m\(=\dfrac{5\sqrt{7}}{4}\)
Vậy tọa độ M thỏa mãn là \(\left(\dfrac{5\sqrt{7}}{4};\dfrac{9}{4}\right)\)và\(\left(\dfrac{5\sqrt{7}}{4};-\dfrac{9}{4}\right)\)
Trong mặt phẳng tọa độ Oxy, cho elip (E) : \(\dfrac{x^2}{25}+\dfrac{y^2}{9}=1\). Gọi hai tiêu điểm của (E) là \(F_1,F_2\) và M là điểm thuộc (E) sao cho \(\widehat{F_1MF_2}=60^0\). Tìm tọa độ điểm M và tính diện tích tam giác \(MF_1F_2\) ?
bài 1: cho elip ( E) \(9x^2+25y^2=225\) và đường thẳng d vuông góc với trục lớn tại tiêu điểm bên phải F2 cắt ( E) tại hai điểm M,N. Tìm tọa độ các điểm M,N
bài 2: phương trình chính tắc của E đi qua hai điểm A\(\left(1;\frac{\sqrt{3}}{2}\right)\) B\(\left(0;1\right)\) là
Bài 1:
\(9x^2+25y^2=225\Leftrightarrow\frac{x^2}{25}+\frac{y^2}{9}=1\)
\(\Rightarrow c^2=a^2-b^2=25-9=16\Rightarrow c=4\Rightarrow F_2\left(4;0\right)\)
Đường thẳng qua \(F_2\) vuông góc trục lớn có pt \(x=4\)
\(\Rightarrow9.4^2+25y^2=225\Leftrightarrow25y^2=81\Rightarrow\left[{}\begin{matrix}y=\frac{9}{5}\\y=-\frac{9}{5}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}M\left(4;\frac{9}{5}\right)\\N\left(4;-\frac{9}{5}\right)\end{matrix}\right.\)
Bài 2:
Gọi pt elip có dạng \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)
\(\Rightarrow\left\{{}\begin{matrix}\frac{1}{a^2}+\frac{3}{4b^2}=1\\\frac{0}{a^2}+\frac{1}{b^2}=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b^2=1\\a^2=4\end{matrix}\right.\)
Phương trình elip: \(\frac{x^2}{4}+\frac{y^2}{1}=1\)
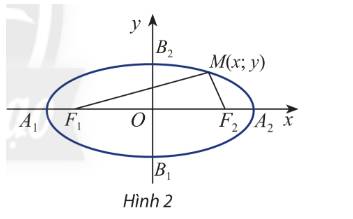
Cho elip (E) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (E) \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \({F_1}M + {F_2}M = 2a \Leftrightarrow \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} + \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} = 2a\)
Cho hyperbol (H) có các tiêu điểm \({F_1}\) và \({F_2}\) và đặt điểm \({F_1}{F_2} = 2c\). Chọn hệ trục tọa độ Oxy sao cho \({F_1}( - c;0)\) và \({F_2}(c;0)\)
Xét điểm \(M(x;y)\)
a) Tính \({F_1}M\) và \({F_2}M\) theo x, y và c
b) Giải thích phát biểu sau:
\(M(x;y) \in (H) \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)

a) Ta có:
\(\overrightarrow {{F_1}M} = \left( {x + c;y} \right) \Rightarrow {F_1}M = \sqrt {{{\left( {x + c} \right)}^2} + {y^2}} \)
\(\overrightarrow {{F_2}M} = \left( {x - c;y} \right) \Rightarrow {F_2}M = \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} \)
b) Ta có \(M(x;y) \in (E)\) nên \(\left| {{F_1}M - {F_2}M} \right| = 2a \Leftrightarrow \left| {\sqrt {{{\left( {x + c} \right)}^2} + {y^2}} - \sqrt {{{\left( {x - c} \right)}^2} + {y^2}} } \right| = 2a\)
cho elip (e) có pt chính tắc: x^2/9 + y^2/4=1
a) tìm tọa độ đỉnh, tiêu điểm f1, f2, và tâm sai của (e)
b) tìm tọa độ điểm m thuộc (e) thõa mãn mf1 -mf2=2
(f1 là tiêu điểm bên trái của elip)
Cho elip (E): x 2 + 9 y 2 = 9
a) Tìm tọa độ hai tiêu điểm của elip
b) Tìm trên (E) điểm M sao cho MF1 = 2MF2
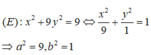
Ta có: c2 = a2 - b2 = 9 - 1 = 8 ⇒ c = 2√2
⇒ F1(-2√2;0), F2(2√2;0)
Tìm trên (E) điểm M sao cho MF1 = 2MF2
Giả sử M(x;y) là điểm thỏa mãn yêu cầu của đề bài
Vì M thuộc (E) nên:
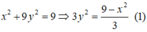
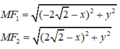
Theo đề bài ta có:
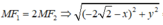
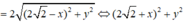
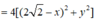
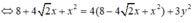
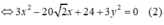
Thay (1) vào (2) ta được:
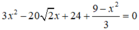
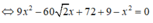
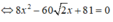
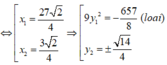
Vậy có hai điểm thỏa mãn đề bài là:
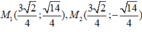
Cho elip \(\left( E \right)\) có phương trình chính tắc \(\frac{{{x^2}}}{{49}} + \frac{{{y^2}}}{{25}} = 1\) .Tìm tọa độ các giao điểm của \(\left( E \right)\) với trục Ox, Oy và tọa độ các tiêu điểm của \(\left( E \right)\).
Từ phương trình chính tắc của (E) ta có: \(a = 7,b = 5 \Rightarrow c = 2\sqrt 6 {\rm{ }}(do{\rm{ }}{{\rm{c}}^2} + {b^2} = {a^2})\)
Vậy ta có tọa độ các giao điểm của (E) với trục Ox, Oy là: \({A_1}\left( { - 7;{\rm{ }}0} \right)\)\({A_2}\left( {7;{\rm{ }}0} \right)\)\({B_1}\left( {0; - {\rm{ 5}}} \right)\)\({B_2}\left( {0;{\rm{ 5}}} \right)\)
Hai tiêu điểm của (E) có tọa độ là: \({F_1}\left( { - 2\sqrt 6 ;0} \right),{F_2}\left( {2\sqrt 6 ;0} \right)\)
Trong mặt phẳng tọa độ Oxy, lập phương trình chính rắc của elip (E) biết (E) có tiêu điểm \(F_1\left(-2;0\right)\) và diện tích hình chữ nhật cơ sở bằng \(12\sqrt{5}\). Viết phương trình đường tròn (C) có tâm là gốc tọa độ và (C) cắt (E) tại bốn điểm tạo thành một hình vuông ?