cho tam giác ABC cân tại A . kẻ AH \(\perp\)BC . lấy M \(\in\)BH . so sánh AH , AM và AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Đường phân giác BD (D∈AC). Kẻ DE\(\perp\) BC(E∈BC)
a)Chứng minh tam giác ABD=tam giác EBD
b)So sánh AD và DC
c)Kẻ AH vuông góc với BC(H∈BC), AH cắt BD tại F. Chứng minh AD song song DE và tam giác ADF cân
Cho tam giác ABC cân tại A, AH vuông góc BC tại H. N là trung điểm AC, BN cắt AH tại G. Trên tia đối NB lấy K cho NK=NG. Cm tam giác BKC là tam giác vuông. So sánh BH và AK.
Giúp m với:))))
Cho tam giác ABC vuông tại A có AB 3cm, AC 4cm.a/ Tính BC. So sánh các góc của tam giác ABC.b/ Từ A kẻ AH vuông góc với BC của tam giác ABC. Trên tia BH lấy điểm D sao cho H là trungđiểm của đoạn thẳng BD.Chứng minh tam giác ABD cân tại A.d) Trên tia AH lấy M sao H là trung điểm AM. Chứng minh : tam giác ABM cân
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm.
a/ Tính BC. So sánh các góc của tam giác ABC.
b/ Từ A kẻ AH vuông góc với BC của tam giác ABC. Trên tia BH lấy điểm D sao cho H là trung
điểm của đoạn thẳng BD.
Chứng minh tam giác ABD cân tại A.
d) Trên tia AH lấy M sao H là trung điểm AM. Chứng minh : tam giác ABM cân
Cho tam giác ABC có đường cao AH. Trên AH lấy điểm D sao cho AD = 2/3 AH. Biết BH = 4cm, BC = 12cm. Nói B với D, nối C với D.
a) So sánh diện tích tam giác ABH và diện tích BDC.
b) Kéo dài BD cắt AC tại M. So sánh AM và MC
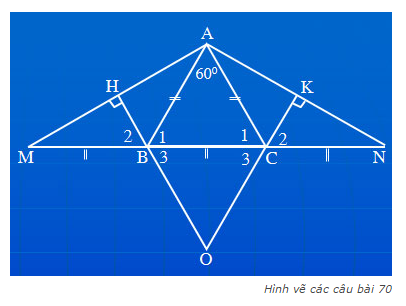
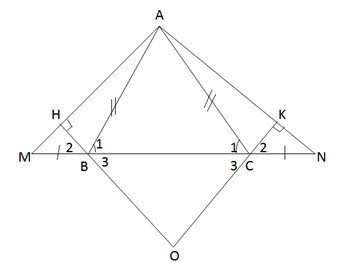
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ BHperp AMleft(Hin AMright), kẻ CKperp ANleft(Kin ANright). Chứng minh rằng BH CK
c) Chứng minh rằng AH AK
d) Khi widehat{BAC}60^0 và BM CN BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC ?
Đọc tiếp
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM = CN
a) Chứng minh rằng tam giác AMN là tam giác cân
b) Kẻ \(BH\perp AM\left(H\in AM\right)\), kẻ \(CK\perp AN\left(K\in AN\right)\). Chứng minh rằng BH = CK
c) Chứng minh rằng AH = AK
d) Khi \(\widehat{BAC}=60^0\) và BM = CN = BC, hãy tính số đo các góc của tam giác AMN và xác định dạng của tam giác OBC ?
a) ∆ABC cân, suy ra ˆB1=ˆC1B1^=C1^
⇒ˆABM=ˆACN⇒ABM^=ACN^
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACNABM^=ACN^
BM = ON (gt)
Suy ra ˆM=ˆNM^=N^
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆNM^=N^ (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2B2^=C2^
Mà ˆB2=ˆB3;ˆC2=ˆC3B2^=B3^;C2^=C3^ (đối đỉnh)
Nên ˆB3=ˆC3B3^=C3^ .
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=600BAC^=600 và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=600BAC^=600 nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=1200ABM^=ACN^=1200 (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=1800−12002=300M^=BAM^=1800−12002=300 .
Suy ra ˆANM=ˆAMN=300ANM^=AMN^=300 .
Và ˆMAN=1800−(ˆAMN+ˆANM)=1800−2.300=1200MAN^=1800−(AMN^+ANM^)=1800−2.300=1200
Vậy ∆AMN có ˆM=ˆN=300;ˆA=1200.M^=N^=300;A^=1200.
+∆BHM có: ˆM=300M^=300 nên ˆB2=600B2^=600 (hai góc phụ nhau)
Suy ra ˆB3=600B3^=600
Tương tự ˆC3=600C3^=600
Tam giác OBC có ˆB3=ˆC3=600B3^=C3^=600 nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).
Đúng 0
Bình luận (1)

a) ∆ABC cân, suy ra ˆB1=ˆC1
⇒ˆABM=ˆACN
∆ABM và ∆CAN có:
AB = AC (gt)
ˆABM=ˆACN
BM = ON (gt)
Suy ra ˆM=ˆN
=>∆AMN là tam giác cân ở A.
b) Hai tam giác vuông ∆BHM và ∆CKN có :
BM = CN (gt)
ˆM=ˆN (CM từ câu a)
Nên ∆BHM = ∆CHN (cạnh huyền, góc nhọn)
Suy ra BH = CK.
c) Theo câu (a) ta có tam giác AMN cân ở A nên AM = AN (*)
Theo câu b ta có ∆BHM = ∆CKN nên suy ra HM = KN (**).
Do đó AH = AM – HM = AN – KN (theo (*) và (**)) = AK
Vậy AH = AK.
d) ∆BHM = ∆CKN suy ra ˆB2=ˆC2
Mà ˆB2=ˆB3;ˆC2=ˆC3 (đối đỉnh)
Nên ˆB3=ˆC3
Vậy ∆OBC là tam giác cân.
e) Khi ˆBAC=60o và BM = CN = BC.
+Tam giác cân ABC có ˆBAC=60o nên là tam giác đều.
Do đó: AB = BC = AC = BM = CN
ˆABM=ˆACN=120o (cùng bù với 600)
∆ABM cân ở B nên ˆM=ˆBAM=180o−120o / 2=30o
Suy ra góc ANM = góc AMN=30o
Và góc MAN=1800−(góc AMN+góc ANM)=1800−2.30o=120o
Vậy ∆AMN có góc M = góc N=30o ; góc A=120o
+∆BHM có: góc M=30o nên góc B2 = 60o (hai góc phụ nhau)
Suy ra góc B3=60o
Tương tự góc C3=60o
Tam giác OBC có góc B3 = góc C3=60o nên tam giác OBC là tam giác đều.
(Tam giác cân có một góc bằng 600 nên là tam giác đều).
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại A(AC> AB).Kẻ AH\(\perp\)BC tại H.Trên tia HC lấy điểm E sao cho HE=AH.Kẻ Ex\(\perp\)BC cắt AC tại F . Chứng minh a)Tam giác ABF vuông cân
b)Gọi M là trung điểm của BF và kẻ FK\(\perp\)AH tại K.Chứng minh tam giác KMH vuông cân.
Cho tam giác ABC (AB < AC) vuông tại A. Đường cao AH. Trên cạnh AC lấy điểm E sao cho AH = AE. Qua E kẻ đường thẳng vuông góc với AC cắt BC tại D
a, Chứng minh tam giác AHD = tam giác AED
b, So sánh DH và DC
c, Gọi DE cắt AH tại K. Chứng minh DKC cân tại C
d, Gọi M là trung điểm của KC. Chứng minh ba điểm A, D, M thẳng hàng
a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
AH=AE
=>ΔAHD=ΔAED
b: ΔAHD=ΔAED
=>DH=DE
mà DE<DC
nên DH<DC
c: Xét ΔDHK vuông tại H và ΔDEC vuông tại E có
DH=DE
góc HDK=góc EDC
=>ΔDHK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
d: AH+HK=AK
AE+EC=AC
mà AH=AE và HK=EC
nên AK=AC
mà DK=DC
nên AD là trung trực của KC
mà M là trung điểm của CK
nên A,D,M thẳng hàng
Đúng 2
Bình luận (0)
cho tam giác abc vuông tại a ab ac có b 60 độ. kẻ ah vuông góc với bc. trên tia hc lấy điểm d sao cho bh=hd
a. c/m △abh=△adh. △abd là tam giác gì?
b. kẻ de vuông góc với ac tại e. so sánh dh và dc?
a: Xét ΔAHB vuông tại H và ΔAHD vuông tại H có
AH chung
HB=HD
=>ΔAHB=ΔAHD
=>AB=AD
mà góc B=60 độ
nên ΔABD đều
b: góc CAD=90-60=30 độ=góc HAD
=>AD là phân giác của góc HAC
=>DH/AH=DC/AC
mà AH<AC
nên DH<DC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC), kẻ AH vuông góc với BC, D thuộc AC sao cho AB=AD kẻ DK vuông góc với AH tại K. Cần chứng minh a) Tam giác ABH= tam giác DAK b) So sánh BH và AD
a: Xét ΔABH vuông tại H và ΔDAK vuông tại K có
AB=DA
góc ABH=góc DAK
=>ΔABH=ΔDAK
b: ΔABH=ΔDAK
=>BH=AK
mà AK<AD
nên BH<AD
Đúng 1
Bình luận (0)