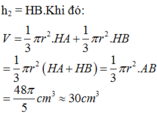Cho tam giác OAB vuông cân tại O, cạnh OA a = . Tính 2OA-OB

Những câu hỏi liên quan
Cho tam giác OAB vuông cân tại O, cạnh OA a. Tính
2
O
A
→
−
O
B
→
.
A. a B.
1
+
2
a
.
C.
a
5
.
D.
2
a...
Đọc tiếp
Cho tam giác OAB vuông cân tại O, cạnh OA= a. Tính 2 O A → − O B → .
A. a
B. 1 + 2 a .
C. a 5 .
D. 2 a 2 .
cho tam giac OAB vuông cân tại A, cạnh OA= a. Tính |3vecto OA + 4vecto OB| theo a
Lời giải:
\(A=|3\overrightarrow{OA}+4\overrightarrow{OB}|\\ \Rightarrow A^2=9OA^2+16OB^2+24\overrightarrow{OA}.\overrightarrow{OB}\)
\(A^2=9a^2+16.2a^2+\overrightarrow{OA}(\overrightarrow{OA}+\overrightarrow{AB})=41a^2+OA^2+\overrightarrow{OA}.\overrightarrow{AB}\\ =41a^2+a^2+0=42a^2\)
(do $OA, AB$ vuông góc với nhau)
$\Rightarrow A=\sqrt{42}a$
Đúng 1
Bình luận (0)
Cho tam giác OAB vuông cân tại O với OA=OB=a. Độ dài của vecto u=12/4 OA - 5/2 OB
tam giác OAB vuông tại O; OB=a;góc OAB =30 quay tam giác đó xung quanh cạnh góc vuông OA ta được một hình gì. Tính diện tích xung quanh của hình đó
Cho tam giác OAB cân tại O. Gọi C và D lần lượt trên 2 cạnh OA và Ob. Sao cho AD vuông góc với OB và BC vuông góc với OA. CMR
a AD=BC và tam giác OCD cân
b Gọi M là giao điểm của BC và AD. CMR OM vuông góc vs AB, OM là tia phân giác góc O
c Chứng minh MA=MB
d CM AB//CD
Trong không gian, cho tam giác OAB vuông tại O có OA 4a, OB 3a. Nếu cho tam giác OAB quay quanh cạnh OA thì mặt nón tạo thành có diện tích xung quanh
S
x
q
bằng bao nhiêu? A.
S
x
q
9
πa...
Đọc tiếp
Trong không gian, cho tam giác OAB vuông tại O có OA = 4a, OB = 3a. Nếu cho tam giác OAB quay quanh cạnh OA thì mặt nón tạo thành có diện tích xung quanh S x q bằng bao nhiêu?
A. S x q = 9 πa 2
B. S x q = 16 πa 2
C. S x q = 15 πa 2
D. S x q = 12 πa 2
Đáp án: C.
§ Hướng dẫn giải:
Dễ thấy h = 4a và r = 3a.
Kết luận diện tích xung quanh là:
S x q = πrl = πr r 2 + h 2 = 15 πa 2
Đúng 0
Bình luận (0)
Cho tam giác OAB vuông tại O, OA 3cm, OB 4cm. Quay tam giác OAB quanh cạnh AB. Thể tích khối tròn xoay được tạo thành gần nhất giá trị nào? A. 28
c
m
3
B. 26
c
m
3
C. 32
c
m
3
D. 30
c
m
3
Đọc tiếp
Cho tam giác OAB vuông tại O, OA = 3cm, OB = 4cm. Quay tam giác OAB quanh cạnh AB. Thể tích khối tròn xoay được tạo thành gần nhất giá trị nào?
A. 28 c m 3
B. 26 c m 3
C. 32 c m 3
D. 30 c m 3
Cho tam giác OAB cân tại O. Kẻ AH vuông góc OB tại H. Kẻ BK vuông góc OA tại K. Gọi I là giao điểm của AH và BK. Chứng minh:
a) ABH = BAK.
b) ABI cân tại I.
a: Xét ΔKAB vuông tại K và ΔHBA vuông tại H có
BA chung
\(\widehat{KAB}=\widehat{HBA}\)(ΔOAB cân tại O)
Do đó: ΔKAB=ΔHBA
b: Ta có: ΔKAB=ΔHBA
=>\(\widehat{KBA}=\widehat{HAB}\)
=>\(\widehat{IAB}=\widehat{IBA}\)
=>ΔIAB cân tại I
Đúng 0
Bình luận (0)
Trong mặt phẳng (P) cho tam giác OAB cân tại
O
,
O
A
O
B
2
a
,
A
O
B
^
120
°
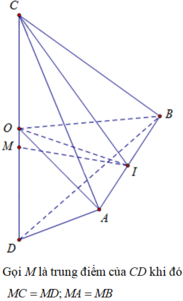
. Trên đường thẳng vuông góc với măt phẳng (P) tại O lấy hai điểm C, D , nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD. A. ...
Đọc tiếp
Trong mặt phẳng (P) cho tam giác OAB cân tại O , O A = O B = 2 a , A O B ^ = 120 ° . Trên đường thẳng vuông góc với măt phẳng (P) tại O lấy hai điểm C, D , nằm về hai phía của mặt phẳng (P) sao cho tam giác ABC vuông tại C và tam giác ABD đều. Tính bán kính mặt cầu ngoại tiếp tứ diện ABCD.
A. 3 a 2 2
B. a 2 3
C. 5 a 2 2
D. 5 a 2 3