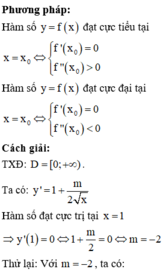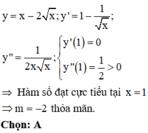Xác định các tham số a,b sao cho hàm số y = \(\frac{ax +b}{x^2+1}\) đạt GTLN = 4 và GTNN = -1

Những câu hỏi liên quan
a, xác định parabol y = ax^2 + bx + c đạt cực tiểu bằng 4 tại x = -2 và đồ thị đi qua A ( 0 ; 6)
b, xác định GTNN của hàm số y = x^2 - 4x + 1
a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)
Đúng 0
Bình luận (0)
Xác định hàm số y = ax² + bx + c biết hàm đạt GTLN bằng 5 tại x = -2 và đồ thị hàm số đi qua điểm M(1; -1)
y = ax2 + bx + c đạt Max bằng 5 tại x = -2
--> a < 0; \(\dfrac{4ac - b^2}{4a}\) = 5;
\(\dfrac{-b}{2a}\) = -2
--> b = 4a; \(\dfrac{4ac - 16a^2}{4a}\) = 5
--> b = c - 5 = 4a
Đồ thị hàm số đi qua M(1; -1)
--> a + b + c = -1
--> a + 4a + 4a + 5 = -1
<=> 9a = -6
<=> a = \(\dfrac{-2}{3}\) --> b = \(\dfrac{-8}{3}\); c = \(\dfrac{7}{3}\)
--> \(y = \dfrac{-2}{3}x^2\ -\)\(\dfrac{8}{3}x\) + \(\dfrac{7}{3}\)
Đúng 0
Bình luận (0)
Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :
a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2
b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.
1. Xác định hàm số bậc nhất $y = ax + b$ biết rằng đồ thị của hàm số đi qua hai điểm $M(1; -1)$ và $N(2;1)$.
2. Cho phương trình $x^2 - 2mx + m^2 - m + 3 = 0$ (1), trong đó $m$ là tham số.
a. Giải phương trình (1) với $m = 4$.
b. Tìm giá trị của $m$ để phương trình (1) có hai nghiệm $x_1$; $x_2$ và biểu thức $P = x_1 x_2 - x_1 - x_2$ đạt giá trị nhỏ nhất.
1.
Vì đồ thị hàm số đi qua điểm nên
và đi qua điểm nên .
Ta có hệ phương trình .
Vậy hàm số cần tìm là
2.a
Với , phương trình trở thành: .
nên phương trình có hai nghiệm phân biệt và .
2.b.
Ta có .
Phương trình (1) có hai nghiệm , khi
Với , áp dụng định lí Vi-et
Ta có: .
Vì nên suy ra .
Dấu "=" xảy ra khi và chỉ khi
Xem thêm câu trả lời
cho hàm số y=x2
a. vẽ đồ thị hàm số
b. xác định các số a,b sao cho đường thẳng y=ax+b cat trục tung tại một diểm có tung dộ bằng 2 và cắt đồ thị hàm số đã cho tại một điểm có hoành độ bằng 1
Xác định tham số m sao cho hàm số y = x +m\(\sqrt{x}\) đạt cực trị tại x = 1
\(y'=1+\dfrac{m}{2\sqrt{x}}\)
Hàm có cực trị tại \(x=1\) khi \(y'=0\) có nghiệm \(x=1\)
\(\Rightarrow1+\dfrac{m}{2\sqrt{1}}=0\Rightarrow m=-2\)
Đúng 1
Bình luận (2)
Xác định các hệ số a,b,c của hàm số y=f(x)=ax^2+bx+c , biết f(0)=1, f(1)=2 và f(2)=4
Theo de ta co:
f(0) = a.02+b.0+c = c =1
f(1)=a.12+b.1+c = a+b+1 = 2 => a+b = 1
f(2)=a.22+b.2+c = 4a+2b+1=2(2a+b)+1 = 4 => 2(2a+b) = 3 => 2a+b = 3/2 => b = 3/2 - 2a
Thay b=3/2 - 2a vao bieu thuc: a+b=1 ta duoc:
a+3/2-2a = 1
3/2-a= 1
=> a = 3/2 - 1 = 1/2
Suy ra: b = 3/2 - 2.1/2 = 1/2
Vay: a = 1/2 ; b=1/2 ; c=1
Đúng 0
Bình luận (0)
Xác định các hệ số a và b để đồ thị của hàm số y = ax + b đi qua các điểm sau
P(4; 2) và Q(1; 1)
Xác định giá trị của tham số m sao cho hàm số y = x + m x đạt cực trị tại x = 1
A. m = -2
B. m = 2
C. m = 6
D. m = -6