Cho tam giác ABC: điểm M thuộc cạnh AB sao cho MB/MC = 1/2. Đường thẳng đi qua M song song với AC và cắt AB tại D. Đường thẳng đi qua M song song với AB và cắt AB tại E. Chu vi tam giác ABC bằng 24cm. Tính chu vi tam giác DBM, chu vi tam giác EMC
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MB/MC=1/2.
Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 24cm, tính chu vi của các tam giác DBM và EMC.
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên MC=2MB
Ta có: MB+MC=BC(M nằm giữa B và C)
nên BC=2MB+MB=3MB
hay \(\dfrac{MB}{BC}=\dfrac{1}{3}\)
Xét ΔABC có
M∈BC(gt)
D∈AB(gt)
MD//AC(gt)
Do đó: ΔBMD\(\sim\)ΔBCA(Định lí tam giác đồng dạng)
⇒\(\dfrac{C_{BMD}}{C_{BCA}}=\dfrac{BM}{BC}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{BMD}}{24}=\dfrac{1}{3}\)
hay \(C_{DBM}=8\left(cm\right)\)
Ta có: \(\dfrac{MB}{MC}=\dfrac{1}{2}\)(gt)
nên \(MB=\dfrac{1}{2}MC\)
Ta có: MB+MC=BC(M nằm giữa B và C)
nên \(BC=\dfrac{1}{2}MC+MC=\dfrac{3}{2}MC\)
hay \(\dfrac{MC}{BC}=\dfrac{2}{3}\)
Xét ΔCBA có
M∈BC(gt)
E∈CA(Gt)
ME//AB(gt)
Do đó: ΔCME∼ΔCBA(Định lí tam giác đồng dạng)
\(\Leftrightarrow\dfrac{C_{CME}}{C_{CBA}}=\dfrac{CM}{CB}\)(Tỉ số chu vi giữa hai tam giác đồng dạng)
⇔\(\dfrac{C_{CME}}{24}=\dfrac{2}{3}\)
hay \(C_{CME}=\dfrac{48}{3}=16\left(cm\right)\)
Vậy: \(C_{DBM}=8\left(cm\right)\); \(C_{CME}=16\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MB/MC = 1/2. Đường thẳng đi qua M và song song với AC cắt AB tại D. Đường thẳng đi qua M song song với AB cắt AC tại E.
a/ chứng minh tứ giác ADME là hình bình hành
b/ tìm các cặp tam giác đồng dạng và tỉ số đồng dạng
c/ tính chu vi tam giác DBM biết chu vi tam giác ABC bằng 24cm
Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho \(\dfrac{BM}{MC}=\dfrac{1}{2}\) . Qua M kẻ đường thẳng song song với AC cắt AB ở D. Qua M kẻ đường thẳng song song với AB cắt AC tại E. Tìm các cặp tam giác đồng dạng.
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho
M
B
M
C
1
2
. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là A.
1
2
B.
1
3
C.
2...
Đọc tiếp
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho M B M C = 1 2 . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Tỉ số chu vi hai tam giác ΔDBM và ΔEMC là
A. 1 2
B. 1 3
C. 2 3
D. 1 4
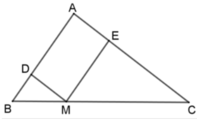
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C (1)
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C (2)
Từ (1) và (2) suy ra:
P B D M P A B C : P E M C P A B C = 1 3 : 2 3 ⇔ P B D M P E M C = 1 2
Đáp án: A
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho
M
B
M
C
1
2
. Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là A. 10cm; 15cm B. 12cm; 16cm C. 20cm; 10cm D. 10cm; 20cm
Đọc tiếp
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho M B M C = 1 2 . Đường thẳng đi qua M và song song với AC cắt AB ở D. Đường thẳng đi qua M và song song với AB cắt AC ở E. Biết chu vi tam giác ABC bằng 30cm. Chu vi của các tam giác DBM và EMC lần lượt là
A. 10cm; 15cm
B. 12cm; 16cm
C. 20cm; 10cm
D. 10cm; 20cm
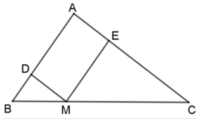
Ta có: MD // AC nên ΔDBM ~ ΔABC. Suy ra :
D B A B = B M B C = D M A C = D B + B M + D M A B + B C + C A
Do đó 1 3 = P B D M P A B C
Chu vi ΔDBM bằng 30. 1 3 = 10cm
Ta có ME // AB nên ΔEMC ~ ΔABC. Suy ra
E M A B = M C B C = E C A C = E M + M C + E C A B + B C + A C
do đó 2 3 = P E M C P A B C
Chu vi ΔEMC bằng 30. 2 3 = 20 cm
Vậy chu vi ΔDBM và chu vi ΔEMC lần lượt là 10cm; 20cm
Đáp án: D
Đúng 0
Bình luận (0)
Cho tam giác ABC. Điểm M thuộc cạnh BC sao cho\(\dfrac{BM}{MC}=\dfrac{1}{2}\) . Qua M kẻ đường thẳng song song với AC cắt AB ở D. Qua M kẻ đường thẳng song song với AB cắt AC tại E. Tính chu vi các tam giác DBM, EMC biết chu vi tam giác ABC bằng 24cm.
Cho tam giác ABC, điểm M thuộc cạnh BC sao cho MB/MC = 1/2. Đường thẳng đi qua M và song song với AC cắt AB tại D. Đường thẳng đi qua M song song với AB cắt AC tại E. Tính tỉ số chu vi của hai tam giác DBM và tam giác EMC
Xem chi tiết
cho tam giác ABC, d là đường thẳng đi qua B, E thuộc AC. Qua E vẽ các đường thẳng song song với AB và BC cắt d tại M,N. D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC tại F và K. CMR tam giác AFN đồng dạng với tam giác MDC
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S là diện tích của tam giác DBC
Chứng minh rằng : dfrac{S}{S}dfrac{DK}{AH}
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và son...
Đọc tiếp
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S' là diện tích của tam giác DBC
Chứng minh rằng : \(\dfrac{S'}{S}=\dfrac{DK}{AH}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T
Chứng minh rằng \(\dfrac{MH}{AD}+\dfrac{MK}{BE}+\dfrac{MT}{CF}=\)



















