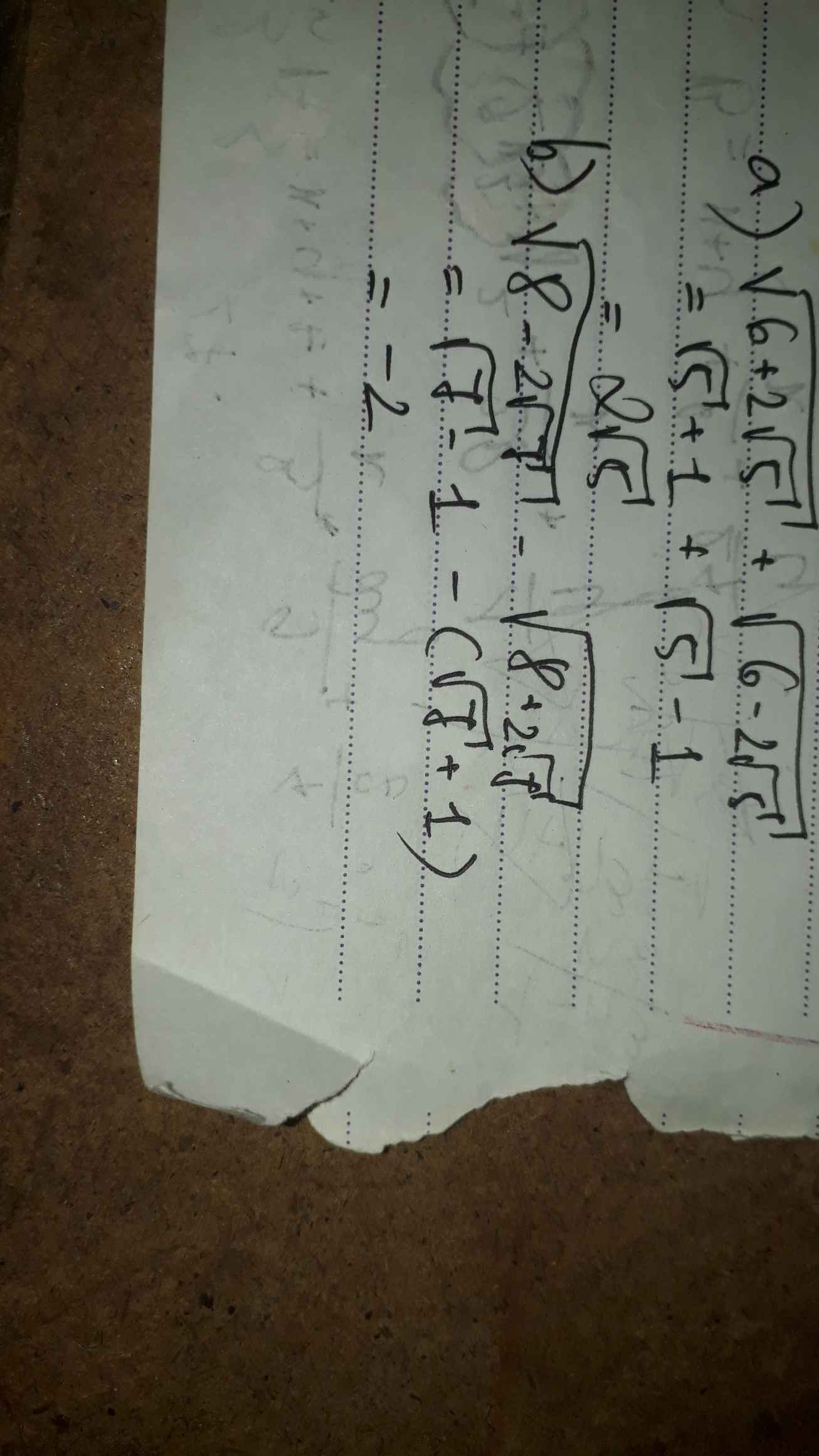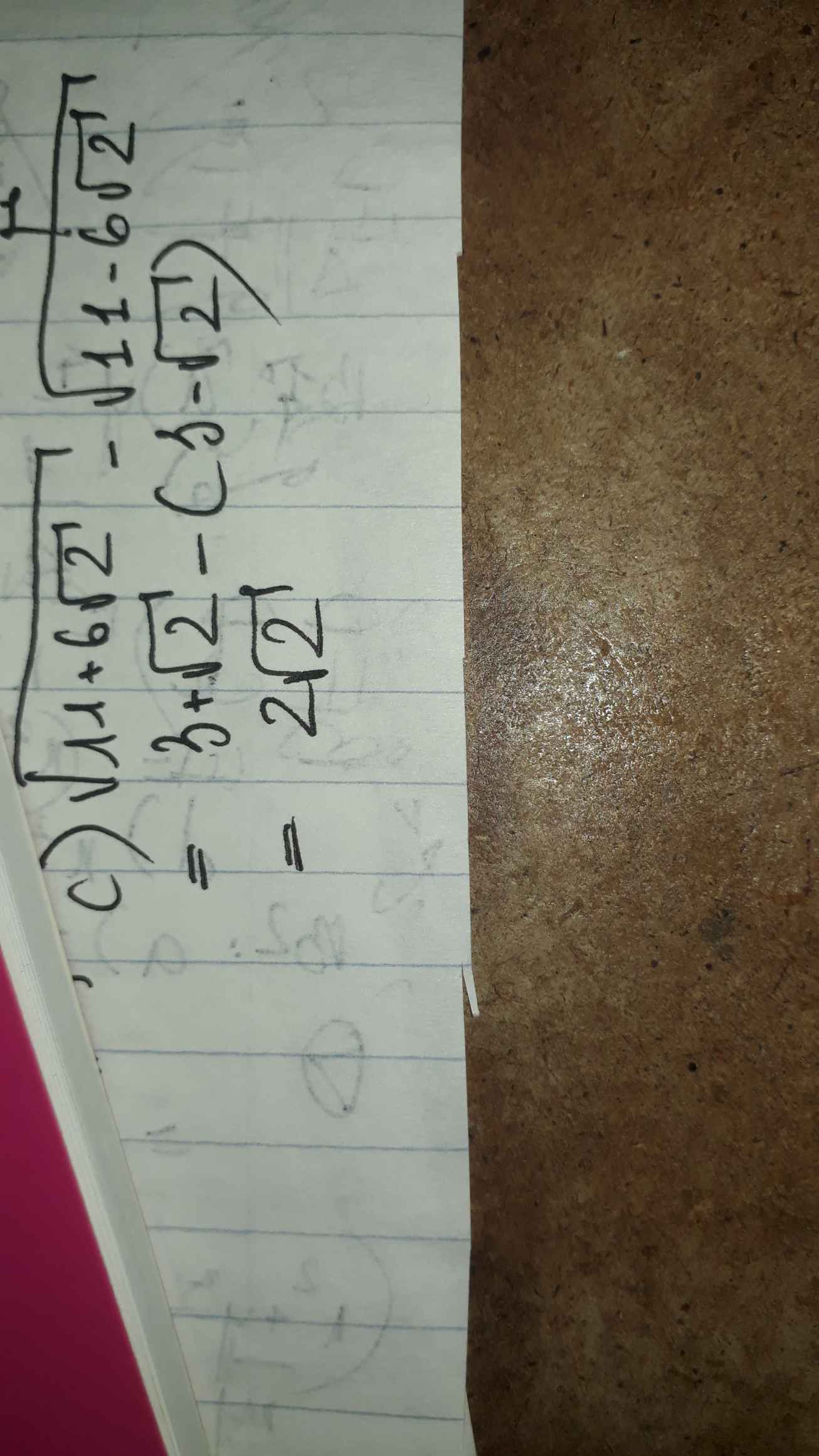M.n giải hộ em vs đg cần gấp ạ
M.n giải hộ em vs đg cần gấp ạ![]()

Những câu hỏi liên quan
mọi người giải hộ e vs ạ!! em đg cần gấp,cảm ơn ạ :333
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
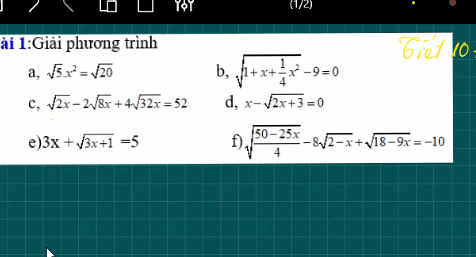
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
Đúng 0
Bình luận (0)
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
Đúng 0
Bình luận (0)
Làm hộ em vs ạ em đg cần gấp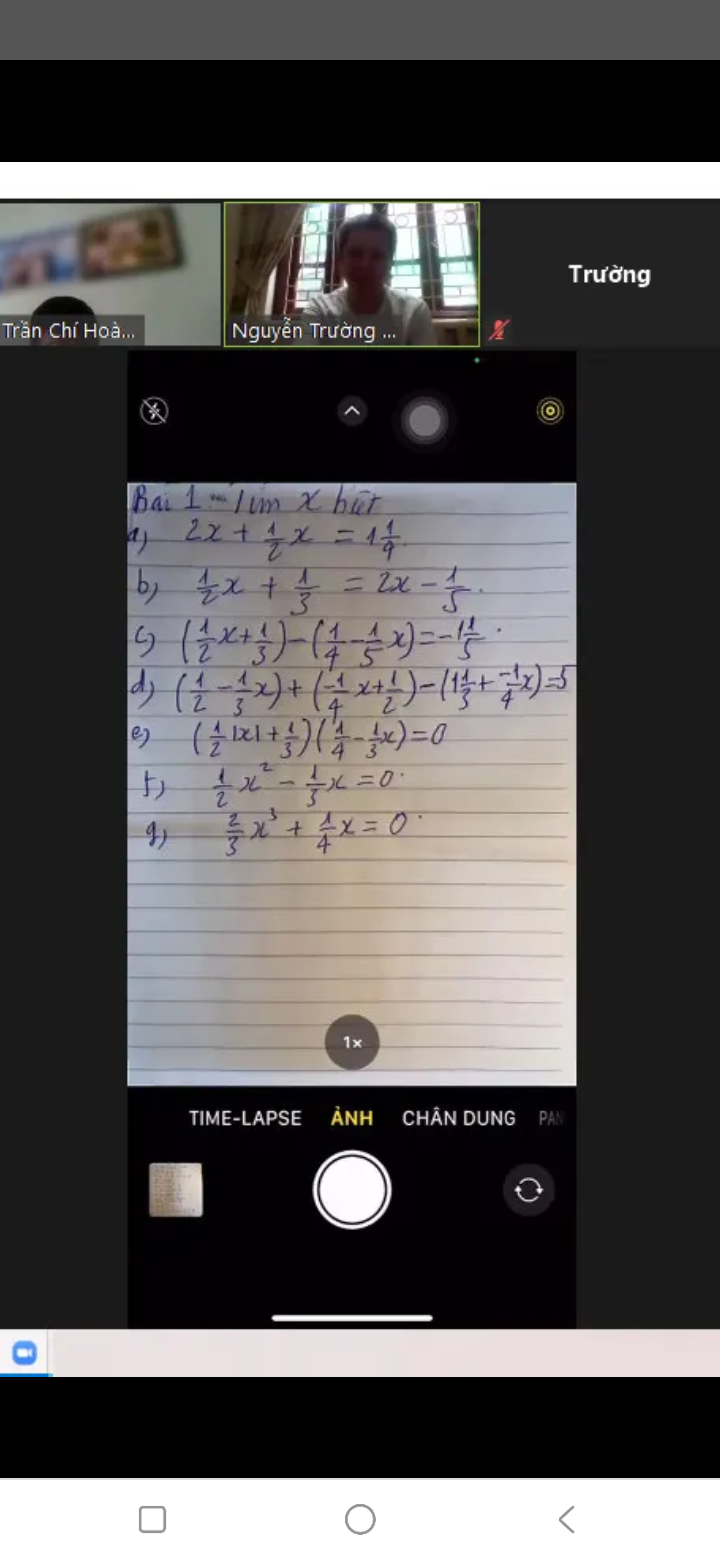
Giải hộ mình vs ạ ! Mình đg cần gấp để nộp 

a) Xét ΔABC vuông tại A và ΔFEC vuông tại F có
\(\widehat{ECF}\) chung
Do đó: ΔABC\(\sim\)ΔFEC(g-g)
Suy ra: \(\dfrac{CA}{CF}=\dfrac{CB}{CE}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(CA\cdot CE=CB\cdot CF\)(Đpcm)
Đúng 0
Bình luận (0)
b) Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=12^2+16^2=400\)
hay BC=20(cm)
Đúng 0
Bình luận (0)
b) Ta có: \(CA\cdot CE=CB\cdot CF\)(cmt)
nên \(CF=\dfrac{CA\cdot CE}{CB}=\dfrac{16\cdot11}{20}=8.8\left(cm\right)\)
Vậy: CF=8,8cm; BC=20cm
Đúng 0
Bình luận (0)

giải hộ mình bài 3 vs ạ!!mình đg cần gấp!!!
Bài 3:
a: Ta có: \(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}+1+\sqrt{5}-1\)
\(=2\sqrt{5}\)
b: Ta có: \(\sqrt{8-2\sqrt{7}}-\sqrt{8+2\sqrt{7}}\)
\(=\sqrt{7}-1-\sqrt{7}-1\)
=-2
c: Ta có: \(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
Đúng 0
Bình luận (0)
Giải hộ mình 3 bài vs ạ ! Mình đg cần gấp để nộp !

16)
a) Tam giác ABC vuông tại A : \(AB^2+AC^2=BC^2\)
BC=10 ⇒FC=10-5.2=4.8
b) Tam giác ABC và tam giác FEC có
C chung
\(\dfrac{AC}{FC}=\dfrac{BC}{EC}=0.6\)
Do đó tam giác ABC đồng dạng với tam giác FEC (C-G-C)
c)⇒Góc FEC=ABC=AEM
Tam giác MAE và tam giác MFB có
Góc M chung
Góc AEM = MBF (CMT)
⇒ 2 Tam giác đồng dạng (G-G)
⇒\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)⇒ MA.MB=MF.MB
Đúng 1
Bình luận (0)
a) Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) (Định lí Py-ta-go)
=> \(BC^2=6^2+8^2=100\)
=> BC = 10 (cm)
=> CF = BC\(-\)BF = 10 - 5,2 = 4,8 (cm)
Vậy BC = 10 cm ; CF = 4,8 cm
b) Xét \(\Delta CAB\) và \(\Delta CFE\) có
\(\left\{{}\begin{matrix}\widehat{C}:chung\\\dfrac{CF}{CE}=\dfrac{CA}{CB}\left(\dfrac{4,8}{6}=\dfrac{8}{10}=\dfrac{4}{5}\right)\end{matrix}\right.\)
=>\(\Delta CAB\sim\Delta CFE\) (c-g-c)
Vậy \(\Delta CAB\sim\Delta CFE\)
c) Xét \(\Delta MAEvà\Delta MFB\) có
\(\left\{{}\begin{matrix}\widehat{M}:chung\\\widehat{MAE}=\widehat{MFB}=90^0\end{matrix}\right.\)
=> \(\Delta MAE\sim\Delta MFB\) (g-g)
=> \(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=> MA.MB = MF.ME
Vậy MA.MB = ME.MF
d) Xét \(\Delta BMF\) và \(\Delta BCA\) có
\(\left\{{}\begin{matrix}\widehat{B}:chung\\\widehat{BFM}=\widehat{BAC}=90^0\end{matrix}\right.\)
=> \(\Delta BMF\) \(\sim\)\(\Delta BCA\) (g-g)
=> \(\dfrac{MF}{AC}=\dfrac{BF}{BA}\)
=> MF = \(\dfrac{8.5,2}{6}\) = \(\dfrac{104}{15}\approx6,9\left(cm\right)\)
Vậy MF \(\approx6,9\left(cm\right)\)
Đúng 0
Bình luận (0)
Bài 18:
*Tính BC
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=21^2+28^2=1225\)
hay BC=35(cm)
Vậy: BC=35cm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho Hình chữ nhật ABCD có AB=8cm , AD =6cm . KẺ AH vuông góc vs BD tại H . tTính BD , AH , BH , CH , DH( vẽ hÌNH HỘ MK NỮA NHÉ0
.. em đg cần gấp mong m.n giúp e vs ạ..e xjn cảm ơn
ai giúp em điền từ trg ngoặc phân tích là loại từ gì và tại sao điền từ đó m.n giúp em đc câu nào giúp em vs đg cần gấp ạ
Mong mn giúp em giải pt này vs ạ! Em đg cần gấp lắm ạ ! Em cảm ơn
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
Đúng 1
Bình luận (0)
Bài 2 ạ lm hộ vs đg cần gấp đấy ạ
Bài 2:
Gọi K là trung điểm của AD và O là trung điểm của BC
Xét ΔABC có
P là trung điểm của AC
O là trung điểm của BC
Do đó: PO là đường trung bình của ΔABC
Suy ra: PO//AB
hay PO//CD
Xét ΔDAB có
K là trung điểm của AD
Q là trung điểm của BD
Do đó: KQ là đường trung bình của ΔDAB
Suy ra: KQ//AB
hay KQ//CD
Xét ΔBDC có
Q là trung điểm của BD
O là trung điểm của BC
Do đó: QO là đường trung bình của ΔBDC
Suy ra: QO//DC
Ta có: QO//DC
mà PO//DC
và QO,PO có điểm chung là O
nên Q,P,O thẳng hàng
Ta có: KQ//CD
QO//CD
mà KQ và QO có điểm chung là Q
nên K,Q,O thẳng hàng
mà Q,P,O thẳng hàng
nên K,Q,P,O thẳng hàng
hay QP//DC(1)
Xét ΔEAB có
M là trung điểm của EA
N là trung điểm của EB
Do đó: MN là đường trung bình của ΔEAB
Suy ra: MN//AB
hay MN//DC(2)
Từ (1) và (2) suy ra MN//PQ
Xét tứ giác MNPQ có MN//PQ
nên MNPQ là hình thang
Đúng 0
Bình luận (0)