Cho tam giác ABC vuông tại A. Trên tia đối của tia CA lấy điểm D sao cho CA=CD. Trên tia đối của tia CB lấy điểm E sao cho CE=CB
a) Tính góc CDE
b)Cho AC=3cm và góc ABC=400. Tính CD và góc DCE
Những câu hỏi liên quan
Cho tam giác ABC vuông ở A . Trên tia đối của tia CA lấy điểm D sao cho CD = CA . Trên tia đối của tia CB lấy điểm E sao cho CE = CD
a) tính góc CDE
b)Cho AC = 3cm , góc ABC = 40 độ Tính DC và góc DEC
Xét tam giác ABC và tam giác DEC có
CB=CE(gt)
góc BCA = góc ECD ( đđ )
CA=CD (gt)
=> tam giác ABC = tam giác DEC (cgc)
=> góc CDE = góc CAB
b) ta có tam giác ABC = tam giác DEC (cmt)
=> AD=DC=3(cm) (cctư)
góc ABC= góc DEC = 40o
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A . Trên tia đối của tia CA lấy điểm D sao cho CD = CA . Trên tia đối của tia CB lấy điểm E sao cho CE = CD
a) tính góc CDE
b)Cho AC = 3cm , góc ABC = 40 độ Tính DC và góc DEC
a: Xét tứ giác AEDB có
C là trung điểm của AD
C là trung điểm của EB
Do đó: AEDB là hình bình hành
Suy ra: AB//DE
=>DE\(\perp\)AC
hay \(\widehat{CDE}=90^0\)
b: DC=AC=3(cm)
\(\widehat{DEC}=\widehat{ABC}=40^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính góc CDE
Xét ΔBAC và ΔEDC có
CB=CE
\(\widehat{BCA}=\widehat{ECD}\)
CA=CD
Do đó: ΔBAC=ΔEDC
Suy ra: \(\widehat{CDE}=90^0\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính góc CDE
Xét ΔCAB và ΔCDE có
CA=CD
\(\widehat{ACB}=\widehat{DCE}\)
CB=CE
Do đó: ΔCAB=ΔCDE
Suy ra: \(\widehat{CAB}=\widehat{CDE}\)
hay \(\widehat{CDE}=90^0\)
Đúng 0
Bình luận (1)
Tam giác ABC có góc A = 90 độ . Trên tia đối của tia CA lấy điểm D sao cho CD = CA . Trên tia đối của tia CB lấy điểm E sao cho CE = CB
a.tính góc CDE
b.cho AC = 3 cm , góc ABC = 40 độ . Tính DC , góc DCE
a) xét tam giác ABC và tam giác DCE có:
AC=CD(gt)
góc ACB = góc DCE (2 góc đối đỉnh)
BC=CE(gt)
=> tan giác ABC = tam giác DEC(c-g-c)
=>góc BAC = góc EDC=90 độ(2 góc tương ứng)
b)Vì tam giác ABC = tam giác DEC
=>AC=CD=3 cm(2 cạnh tương ứng)
Xét tam giác ABC vuông tại A có:
góc ABC+ góc ACB=90độ
40độ + góc ACB=90độ
góc ACB=50độ
=>góc DCE=50độ(vì góc ACB= góc DCE do 2 góc đối đỉnh)
Vậy DC=3 cm;góc DCE=50độ
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A= 90o. Trên tia đối của tia CA lấy điểm D sao cho CD=CA. Trên tia đối CB lấy điểm E sao cho CE = CB. Vẽ hình và tính số đo góc CDE.
Xét tứ giác ABDE có
C là trung điểm của AD
C là trung điểm của BE
Do đó: ABDE là hình bình hành
Suy ra: AB//DE
hay DE⊥AC
=>\(\widehat{CDE}=90^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia đối của tia CA lấy điểm D sao cho CD=CA. Trên tia đối của tia CB lấy điểm E sao cho CE=CB.
a) Tính số đo góc CDE;
b) Cho AC = 3cm và ABC = 40o. Tính DC và DCE.
Các bạn giúp mik bài này với
Ta có hình vẽ:
a) Xét Δ BCA và Δ ECD có:
CA = CD (gt)
BCA = ECD (đối đỉnh)
CB = CE (gt)
Do đó, Δ BCA = Δ ECD (c.g.c)
=> CAB = CDE = 90o (2 góc tương ứng)
b) Có: AC = DC = 3 (gt)
Δ ABC vuông tại A có: ABC + BCA = 90o
=> 40o + BCA = 90o
=> BCA = 90o - 40o = 50o = DCE (đối đỉnh)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Trên tia đối của tia CA, lấy điểm D sao cho cho CA = CD. Trên tia đối của tia CB, lấy điểm E sao cho CB = CE. Số đo góc C D E ^ là:
A. 80 °
B. 90 °
C. 100 °
D. 110 °
Cho tam giác ABC có ∠A =90o. Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo góc CDE
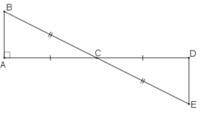
Xét ΔABC và ΔDEC, ta có:
AC = DC (gt)
∠(ACB) =∠(ECD) (đối đỉnh)
BC=EC (gt)
Suy ra: ΔABC= ΔDEC (c.g.c)
⇒∠A =∠D ̂(hai góc tương ứng).Mà ∠A =90o nên ∠D =90o
Đúng 1
Bình luận (0)
Xét △ABC và △DEC
(c)AC=CD (gt)
(g)∠BCA=∠ECD (vì đối đỉnh)
(c)BC=CE (gt)
vậy ΔABC=ΔDEC (c-g-c)
⇒ ∠CDE=∠BAC=900 (2 cạnh tương ứng)
nhớ tick đúng giùm
Đúng 1
Bình luận (0)
Bài 4: Cho tam giác ABC có góc A = 90 độ . Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. a) Chứng minh tam giác ABC = tam giác DEC
b) Tính số đo góc CDE ?
Xét tamgiac ABC và tam giác DEC
AC=CD (gt)
BCA=ECD (đđ)
BC=CE (gt)
Vậy tam giác ABC=tam giác DEC (c-g-c)
⇒ CDE=BAC=90 (tương ứng)
Đúng 1
Bình luận (0)