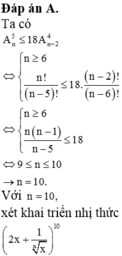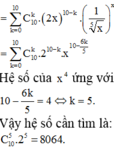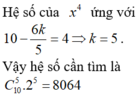tìm hệ số của x4 y9 trong khai triển (2x-y) 13

Những câu hỏi liên quan
1. Tìm hệ số của số hạng x^4 trong khai triển left(x-3right)^92. Tìm hệ số của số hạng chứa x^{12}y^{13} trong khai triển left(2x+3yright)^{25}3. Tìm hệ số của số hạng chứa x^4 trong khai triển left(dfrac{x}{3}-dfrac{3}{x}right)^{12}4. Tìm hệ số của số hạng không chứa x trong khai triển left(x^2-dfrac{1}{x}right)^65. Tìm hệ số của số hạng không chứa x trong khai triển left(x+dfrac{1}{x^4}right)^{10}
Đọc tiếp
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Tìm hệ số của x4 trong khai triển biểu thức (2x+1)(x-1)5
Hệ số của x^4 sẽ là tổng của 2*a và 1*b, với a là hệ số của x^3 trong (x-1)^5, b là hệ số của x^4 trong (x-1)^5
SHTQ là: \(C^k_5\cdot x^{5-k}\cdot\left(-1\right)^k=C^k_5\cdot\left(-1\right)^k\cdot x^{5-k}\)
Số hạng chứa x^3 tương ứng với 5-k=3
=>k=2
=>Hệ số là \(C^2_5\cdot\left(-1\right)^2=10\)
Số hạng chứa x^4 tương ứng với 5-k=4
=>k=1
=>Hệ số là \(C^1_5\cdot\left(-1\right)=-5\)
=>Hệ số của x^4 là: 2*10+1*(-5)=20-5=15
Đúng 0
Bình luận (0)
Tìm hệ số của x4 trong khai triển sau thành đa thức ( 1+2x+3x2)10
Cho n là số nguyên dương thỏa mãn
5
C
n
1
−
C
n
2
5.
Tìm hệ số a của
x
4
trong khai triển của biểu thức
2
x
+
1
x
2...
Đọc tiếp
Cho n là số nguyên dương thỏa mãn 5 C n 1 − C n 2 = 5. Tìm hệ số a của x 4 trong khai triển của biểu thức 2 x + 1 x 2 n .
A. a = 11520.
B. a = 256.
C. a = 45.
D. a = 3360.
Đáp án A.
Phương pháp:
+) Tổ hợp chập k của n phần tử:
C n k = n ! n − k ! k ! .
+) Công thức khai triển nhị thức Newton:
x + y n = ∑ i = 0 n C n i x i . y n − i .
Cách giải:
5 C n 1 − C n 2 = 5 , n ∈ N , n ≥ 2
⇔ 5 n − n n − 1 2 = 5 ⇔ 10 n − n 2 + n = 0 ⇔ n 2 − 1 ln + 10 = 0 ⇔ n = 10
Khi đó,
2 x + 1 x 2 n = 2 x + x − 2 10 = ∑ i = 0 10 C 10 i 2 x i . x − 2 10 − i = ∑ i = 0 10 C 10 i 2 i x 3 i − 20
Số hạng chứa x 4 trong khai triển ứng với i thỏa mãn
3 i − 20 = 4 ⇔ i = 8
Hệ số a của x 4 trong khai triển:
a = C 10 8 2 8 = 11520.
Đúng 0
Bình luận (0)
Tìm hệ số của
x
4
trong khai triển nhị thức Newton
2
x
+
1
x
5
n
với
x
0
biết n là số tự nhiên lớn nhất thỏa mãn
A
n
5
≤
18...
Đọc tiếp
Tìm hệ số của x 4 trong khai triển nhị thức Newton 2 x + 1 x 5 n với x > 0 biết n là số tự nhiên lớn nhất thỏa mãn A n 5 ≤ 18 A n - 2 4
A. 8064
B. 3360
C. 13440
D. 15360
Tìm hệ số của
x
4
trong khai triển nhị thức Newton
2
x
+
1
x
5
n
với x 0, biết n là số tự nhiên lớn nhất thỏa mãn
A
n
5
≤
18
A...
Đọc tiếp
Tìm hệ số của x 4 trong khai triển nhị thức Newton 2 x + 1 x 5 n với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn A n 5 ≤ 18 A n - 2 4 .
A. 8064
B. 3360
C. 13440
D. 15360
Đáp án A.
Ta có A n 5 ≤ 18 A n - 2 4 ⇔ n ≥ 6 n ! n - 5 ! ≤ 18 . n - 2 ! n - 6 ! ⇔ n ≥ 6 n n - 1 n - 5 ≤ 18 ⇔ 9 ≤ n ≤ 10 → n = 10 .
Với n = 10, xứt khai triển nhị thức
2 x + 1 x x 10 = ∑ k = 10 10 C 10 k . 2 x 10 - k . 1 x 5 x = ∑ k = 0 10 C 10 k . 2 10 - k . x 10 - 6 k 5 .
Hệ số của x 4 ứng với 10 - 6 k 5 = 4 ⇔ k = 5 . Vậy hệ số cần tìm là C 10 5 . 2 5 = 8064 .
Đúng 0
Bình luận (0)
Tìm hệ số của
x
4
trong khai triển nhị thức Newton
2
x
+
1
x
5
n
với x 0, biết n là số tự nhiên lớn nhất thỏa mãn
A
n
5
≤
18
A...
Đọc tiếp
Tìm hệ số của x 4 trong khai triển nhị thức Newton 2 x + 1 x 5 n với x > 0, biết n là số tự nhiên lớn nhất thỏa mãn A n 5 ≤ 18 A n - 2 4
A. 8064
B. 3360
C. 13440
D. 15360
Tìm hệ số của
x
4
trong khai triển nhị thức Newton
2
x
+
1
x
5
n
với x0, biết n là số tự nhiên lớn nhất thỏa mãn
A
n
5
≤
18
A
n...
Đọc tiếp
Tìm hệ số của x 4 trong khai triển nhị thức Newton 2 x + 1 x 5 n với x>0, biết n là số tự nhiên lớn nhất thỏa mãn A n 5 ≤ 18 A n − 2 4
A. 8064
B. 3360
C. 13440
D. 15360
1. Tìm hệ số của x4 trong khai triển (3x+1)6
\(\left(3x+1\right)^6=\sum\limits^6_{k=0}C^k_6.\left(3x\right)^k=\sum\limits^6_{k=0}C^k_6.3^kx^k\)
\(\Rightarrow k=4\)
\(\Rightarrow\) Hệ số của \(x^4\) trong khai triển \(\left(3x+1\right)^6\) là: \(C^4_6.3^4=1215\)
Đúng 0
Bình luận (0)