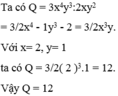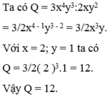\(2xy^2-3xy+x^2-4-C=xy^2-x^2+2y^2+1\)

\(\Rightarrow C=2xy^2-3xy+x^2-4-\left(xy^2-x^2+2y^2+1\right)\)

\(=2xy^2-3xy+x^2-4-xy^2+x^2-2y^2-1\)

\(=xy^2-3xy+2x^2-2y^2-5\)

Thay x = 2 và y = -1 vào C ta được : 

\(C=2.\left(-1\right)^2-3.2.\left(-1\right)+2.2^2-2.\left(-1\right)^2-5=9\)

Vậy : Khi x = 2 và y = -1 thì giá trị của C là -9.

Ta có \(x^4+y^4-1=xy\left(3-2xy\right)\)

\(\Leftrightarrow x^4+y^4-1=3xy-2x^2y^2\)

\(\Leftrightarrow x^4+2x^2y^2+y^4=3xy+1\)

\(\Leftrightarrow\left(x^2+y^2\right)^2=3xy+1\)

Vì \(\left(x^2+y^2\right)^2\ge0\forall x;y\)

\(\Rightarrow3xy+1\ge0\)

\(\Leftrightarrow xy\ge-\frac{1}{3}\)

\(\Leftrightarrow P\ge-\frac{1}{3}\)

Dấu "=" tại x = y = 0

Cái này y hệt cái đề mik thi:)

trời dài thế làm lâu phết đó nha hừm làm theo đúng công thức là được :)

b) 24x^2+6x^2y−2x−12yx−3y^2x+y 

tôi làm theo cách tìm tích số

nếu thấy đúng thì tick cho tôi nha

\(P=\dfrac{4x^2+2xy-\left(x^2+y^2\right)}{2xy-2y^2+3\left(x^2+y^2\right)}=\dfrac{3x^2+2xy-y^2}{3x^2+2xy+y^2}\)

Biểu thức này không tồn tại max mà chỉ tồn tại min

\(P=\dfrac{-2\left(3x^2+2xy+y^2\right)+9x^2+6xy+y^2}{3x^2+2xy+y^2}=-2+\dfrac{\left(3x+y\right)^2}{2x^2+\left(x+y\right)^2}\ge-2\)

Bạn coi lại mẫu số

\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)

\(A=x^2+y^2+\left(\dfrac{1}{2}\right)^2-2xy+2.\dfrac{1}{2}x-2.\dfrac{1}{2}.y+\dfrac{3}{4}\)

\(A=\left(x-y+\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)

\(A_{min}=\dfrac{3}{4}\) khi \(x-y+\dfrac{1}{2}=0\)