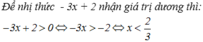Đề sai rồi bạn

\(a,ĐK:x\ge1;x\ne3\\ b,A=\dfrac{\left(\sqrt{x-1}+\sqrt{2}\right)\left(\sqrt{x-1}-\sqrt{2}\right)}{\sqrt{x-1}-\sqrt{2}}=\sqrt{x-1}+\sqrt{2}\)

Lời giải:

ĐKXĐ: $x>0$

Có: $C=\sqrt{x}+\frac{2}{\sqrt{x}}\geq 2\sqrt{2}$ theo BĐT AM-GM

Vậy $C_{\min}=2\sqrt{2}$. Giá trị này đạt tại $\sqrt{x}=\frac{2}{\sqrt{x}}$

$\Leftrightarrow x=2$ 

\(P=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)-\dfrac{x\sqrt{x}+1}{x-\sqrt{x}+1}\) đk: \(x\ge0,x\ne1\)

\(=\dfrac{x+\sqrt{x}+1}{x+1}:\left[\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}\left(x+1\right)-\left(x+1\right)}\right]-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}\)

\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{\left(x+1\right)-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+1\right)}-\left(\sqrt{x}+1\right)\)

\(=\dfrac{x+\sqrt{x}+1}{x+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+1\right)}{\left(\sqrt{x}-1\right)^2}-\left(\sqrt{x}+1\right)\)

\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)

\(=\dfrac{x+\sqrt{x}+1-\left(x-1\right)}{\sqrt{x}-1}\)

\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\)

b)Để P<4 \(\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-1}< 4\) \(\Leftrightarrow\dfrac{\sqrt{x}+2}{\sqrt{x}-1}-4< 0\) \(\Leftrightarrow\dfrac{\sqrt{x}+2-4\left(\sqrt{x}-1\right)}{\sqrt{x}-1}< 0\)

\(\Leftrightarrow\dfrac{6-3\sqrt{x}}{\sqrt{x}-1}< 0\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}6-3\sqrt{x}>0\\\sqrt{x}-1< 0\end{matrix}\right.\\\left\{{}\begin{matrix}6-3\sqrt{x}< 0\\\sqrt{x}-1>0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}< 2\\\sqrt{x}< 1\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}>2\\\sqrt{x}>1\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}< 1\\\sqrt{x}>2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}0\le x< 1\\x>4\end{matrix}\right.\)

Vậy...

c)\(P=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\) \(=1+\dfrac{3}{\sqrt{x}-1}\)

Để P nguyên khi \(\dfrac{3}{\sqrt{x}-1}\) nguyên

\(x\in Z\)\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}\in Z\\\sqrt{x}\in I\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-1\in Z\\\sqrt{x}-1\in I\end{matrix}\right.\)

Tại \(\sqrt{x}-1\in I\Rightarrow\dfrac{3}{\sqrt{x}-1}\notin Z\) (L)

Tại\(\sqrt{x}-1\in Z\) .Để \(\dfrac{3}{\sqrt{x}-1}\in Z\)

\(\Leftrightarrow\sqrt{x}-1\inƯ\left(3\right)=\left\{-1;1;-3;3\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{0;2;-2;4\right\}\) mà \(\sqrt{x}\ge0\)

\(\Rightarrow\sqrt{x}\in\left\{0;2;4\right\}\) \(\Leftrightarrow x\in\left\{0;4;16\right\}\) (tm)

Đáp án: B

P nguyên <=> \(\dfrac{x-5}{\sqrt{x}+1}\) nguyên

<=> \(\dfrac{x-1}{\sqrt{x}+1}-\dfrac{4}{\sqrt{x}+1}\) nguyên

<=> \(\sqrt{x}-1-\dfrac{4}{\sqrt{x}+1}\) nguyên

=> \(\sqrt{x}+1\inƯ\left(4\right)=\left\{1;2;4\right\}\)  (vì \(\sqrt{x}+1>0\forall x\in N\))

...

\(\sqrt{x}+\sqrt{2-x}\le\sqrt{2\left(x+2-x\right)}=2\)

\(\sqrt{x}+\sqrt{2-x}\ge\sqrt{x+2-x}=\sqrt{2}\)

\(\Rightarrow\dfrac{2}{2}\le P\le\dfrac{2}{\sqrt{2}}\Rightarrow1\le P\le\sqrt{2}\)

Mà \(P\in Z\Rightarrow P=1\)

\(\Rightarrow\sqrt{x}+\sqrt{2-x}=2\Rightarrow x=1\)