TẢ TRỤC SỐ
TẢ TRỤC SỐ

Những câu hỏi liên quan
Hình 5 mô tả một vật chuyển động từ điểm gốc O theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm -40 trên trục số (đơn vị đo trên trục số là ki-lô-mét)Hỏi vật đã chuyển động được quãng đường bao nhiêu ki-lô-mét sau 1 giờ?Làm thế nào để biểu diễn được quãng đường đó thông qua số thực -40?
Đọc tiếp
Hình 5 mô tả một vật chuyển động từ điểm gốc O theo chiều ngược với chiều dương của trục số. Sau 1 giờ, vật đến điểm -40 trên trục số (đơn vị đo trên trục số là ki-lô-mét)

Hỏi vật đã chuyển động được quãng đường bao nhiêu ki-lô-mét sau 1 giờ?
Làm thế nào để biểu diễn được quãng đường đó thông qua số thực -40?
Vật đã chuyển động được quãng đường là:
0 – (- 40) = 40 (km)
Để biểu diễn được quãng đường đó thông qua số thực -40, ta sử dụng khái niệm giá trị tuyệt đối (|-40| = 40)
Đúng 0
Bình luận (0)
vật đã đi được 40km sau 1h
biểu diễn bằng cách lấy khoảng cách từ 0 đến -40 trên trục số
Đúng 0
Bình luận (0)
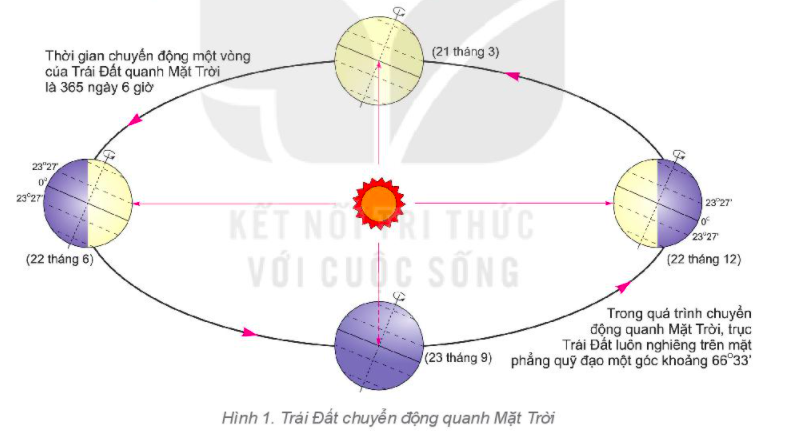
mô tả chuyển động trái đất quanh mặt trời
mô tả chuyển động tự quay quanh trục của trái đất
+ Trái đất quay quanh Mặt Trời theo chiều ngược kim đồng hồ ( Từ tây sang đông )
+ Trái đất quay quanh Mặt Trời 365 ngày 6 giờ ( Dư 6 giờ nên cứ 4 năm lại có 366 ngày )
Đúng 0
Bình luận (0)
-Trái Đất chuyển động một vòng quanh Mặt Trời trên quỹ đạo hết 365 ngày và 6 giờ. -Trong khi chuyển động trên quỹ đạo quanh mặt trời, trục Trái Đất lúc nào cũng giữ nguyên độ nghiêng 66o33' trên mặt phẳng quỹ đạo và hướng nghiêng của trục không đổi. Đó là sự chuyển động tịnh tiến.
Hiện tượng tự quay của Trái Đất là sự quay của hành tinh Trái Đất xung quanh trục của nó. Trái Đất quay từ phía tây sang phía đông. Nhìn từ sao Bắc cực Polaris, Trái Đất quay ngược chiều kim đồng hồ. ... Trái Đất quay một vòng khoảng 24 giờ so với Mặt Trời và 23 giờ, 56 phút và 4 giây so với các ngôi sao
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Trong cùng một hệ trục tọa độ, hãy vẽ
Đường gấp khúc tần suất mô tả bảng phân bố tần suất ghép lớp lập được ở bài tập số 2 theo chiều cao của học sinh nam
Đường gấp khúc tần suất mô tả bảng phân bố tần suất ghép lớp lập được ở bài tập số 2 theo chiều cao của học sinh nữ.
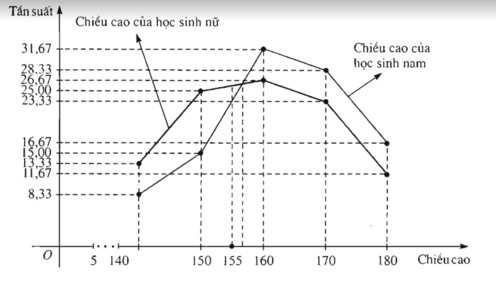
Hình 56. Đường gấp khúc tần suất về chiều cao (cm) của 60 học sinh nam, 60 học sinh nữ.
Đúng 0
Bình luận (0)
em hãy mô tả vận động tự quay quang trục của trái đất
– Trái Đất tự quay quanh một trục tưởng tượng nối liền hai cực và nghiêng 66°33′ trên mặt phẳng quỹ đạo. Hướng tự quay là từ tây sang đông. Thời gian Trái Đất tự quay một vòng quanh trục trong một ngày đêm (hết 24 giờ)
– Hệ quả :
+ Do Trái Đất tự quay quanh trục từ Tây sang Đông nên khắp mọi nơi trên Trái Đất đều lần lượt có ngày, đêm.
+ Sự chuyển động của Trái Đất quanh trục còn làm cho các vật chuyển động trên bề mặt Trái Đất bị lệch hướng.
Đúng 1
Bình luận (0)
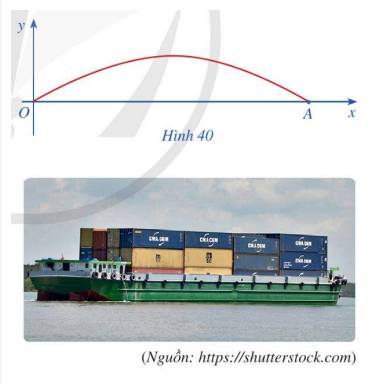
Một cây cầu có dạng cung OA của đồ thị hàm số y 4,8sin frac{x}{9} và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.c) Một sà lan khác cũng...
Đọc tiếp
Một cây cầu có dạng cung OA của đồ thị hàm số \(y = 4,8\sin \frac{x}{9}\) và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 40.
a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (Làm tròn kết quả đến hàng phần mười)
b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1m.
c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3m
Tham khảo:
a) Hai vị trí \(O\) và \(A\) là hai vị trí chân cầu, tại hai vị trí này ta có: \(y = 0\)
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k\pi (k \in \mathbb{Z}) \Leftrightarrow x = 9k\pi (k \in \mathbb{Z})\)
Quan sát đồ thị ta thấy, đồ thị hàm số \({\rm{y}} = 4,8 \cdot \sin \frac{x}{9}\) cắt trục hoành tại điểm 0 và \({\rm{A}}\) liên tiếp nhau với \(x \ge 0\).
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} = 0\);
Xét \({\rm{k}} = 1\), ta có \({{\rm{x}}_2} = 9\pi \).
Mà \({x_1} = 0\) nên đây là hoành độ của 0 , do đó \({x_2} = 9\pi \) là hoành độ của điểm \(A\).
Khi đó \(OA = 9\pi \approx 28,3\).
Vậy chiều rộng của con sông xấp xỉ 28,3 m.
b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với \({\rm{y}} = 3,6\).
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 3,6 \Leftrightarrow \sin \frac{x}{9} = \frac{3}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{\rm{x}}}{9} \approx 0,848 + {\rm{k}}2\pi }\\{\frac{{\rm{x}}}{9} \approx \pi - 0,848 + {\rm{k}}2\pi }\end{array}} \right.\)
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp \(SHIFT\)\sin 3 \div 4 = ta được kết quả gần đúng là 0,85) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{x}} \approx 7,632 + 18{\rm{k}}\pi }\\{{\rm{x}} \approx 9\pi - 7,632 + 18{\rm{k}}\pi }\end{array}({\rm{k}} \in \mathbb{Z})} \right.\)
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} \approx 7,632;{{\rm{x}}_2} \approx 20,642\).
Ta biểu diễn các giá trị \(x\) vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số \(y = \) 4,8. \(\sin \frac{x}{9}\) như sau:
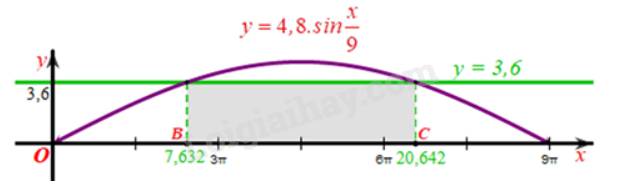
Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng \({\rm{BC}}\) trên hình vẽ.
Mà \(BC \approx 20,642 - 7,632 = 13,01(m) < 13,1(m)\).
Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.
c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:
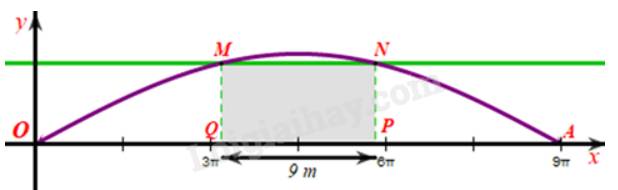
Khi đó \(QP = 9;OA = 28,3\) và \(OQ = PA\).
Mà \(OQ + QP + PA = OA \Rightarrow OQ + 9 + OQ \approx 28,3 \Rightarrow OQ \approx 9,65\)
Khi đó \({y_M} = 4,8 \cdot \sin \frac{{{x_M}}}{9} = 4,8 \cdot \sin \frac{{OQ}}{9} \approx 4,8 \cdot \sin \frac{{9,65}}{9} \approx 4,22(\;{\rm{m}}) < 4,3\) (m).
Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.
Đúng 0
Bình luận (0)
Hãy miêu tả bác cần trục mà em đã nhìn thấy
Bạn Tham Khảo Nhé:~
Khi được đến tham quan bến cảng Hải Phòng, em ấn tượng nhất với những chiếc cần trục ở đây.
Chiếc cần trục được giới thiệu là cỗ máy khổng lồ và tuyệt vời nhất trong bến cảng. Và quả thực đi trên bến cảng, em phải ngước mắt lên nhìn những chiếc cần trục bởi chúng rất cao và đồ sộ như những gã khổng lồ, nổi bật giữa những chiếc xe chở hàng, máy móc tí hon. Mỗi chiếc được mặc một bộ quần áo khác nhau, có chú mặc áo màu đỏ, có anh lại thích khoác trên mình bộ cánh màu vàng nổi bật. Để điều khiển cỗ máy ấy hoạt động trơn tru, linh hoạt, chỉ cần một anh công nhân ngồi trong bệ đỡ của cần trục và điều khiển mọi hoạt động của nó. Khi bốc dỡ hàng hóa từ bến cảng lên tàu và từ tàu xuống bến cảng, chiếc cần trục cứ quay đi quay lại liên tục, nhẹ nhàng dùng chiếc cần của mình móc vào những thùng công-ten-nơ rồi nâng lên hạ xuống rất dễ dàng. Nhìn chúng làm việc nhẹ nhàng như thế nhưng ai biết đâu những thùng hàng trung bình nặng từ vài tấn đến vài chục tấn, nếu không phải máy móc, sức người khó có thể thực hiện đước.
## Chúc Bạn HỌc Tốtt ##
@ Nguyễn Thị Bảo Thuận
Hình 52.2 có mô tả đúng sự quay của Trái Đất quanh trục của nó không?
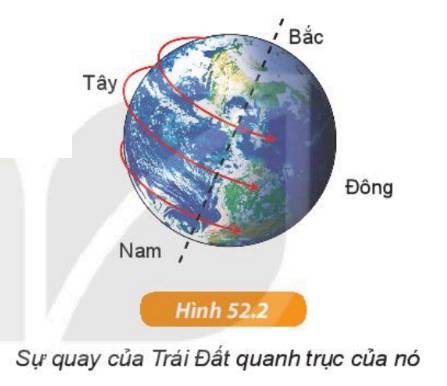
Hình 52.2 mô tả đúng sự quay của Trái Đất quanh trục của nó, từ Tây sang Đông.
Đúng 0
Bình luận (0)
Một vật dao động điều hòa trên trục
O
x
quanh điểm
O
với tần số góc
ω
, biên độ
A
và pha ban đầu
φ
. Phương trình mô tả li độ
x
của vật theo thời gian
t
có dạng A.
x
A
t
cos
ω
+
φ
B.
x...
Đọc tiếp
Một vật dao động điều hòa trên trục O x quanh điểm O với tần số góc ω , biên độ A và pha ban đầu φ . Phương trình mô tả li độ x của vật theo thời gian t có dạng
A. x = A t cos ω + φ
B. x = ω A cos ω t + φ
C. x = A cos ω t + φ
D. x = ω 2 A cos ω t + φ
Đáp án C
Phương trình li độ của vật dao động điều hòa được xác định bằng biểu thức x = A cos ω t + φ
Đúng 0
Bình luận (0)
Từ ngữ nào dưới đây viết sai chính tả?
lang thang
mang vác
trùn trục
trung chuyển
Xem thêm câu trả lời