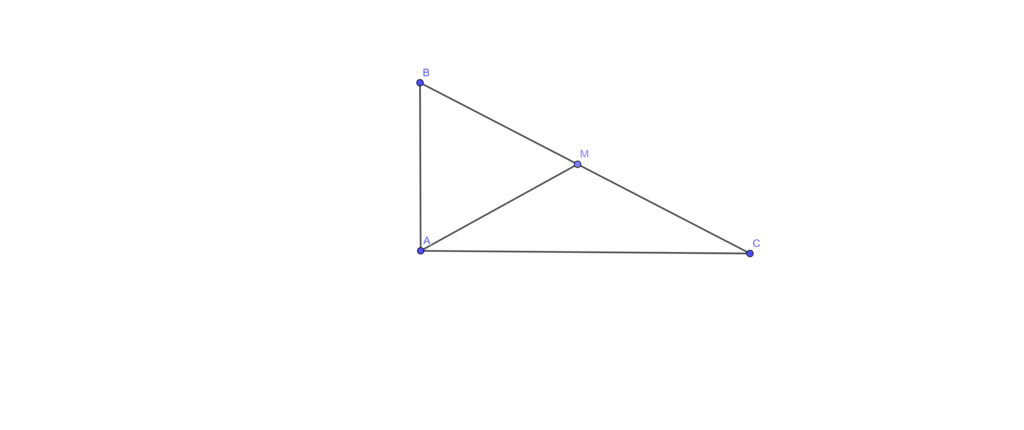
Cho tam giác abc trên bc lấy m cmr:nếu am=bm=cm thì tam giác abc vuông tại a

Những câu hỏi liên quan
cho tam giác abc trên bc lấy m cmr:nếu am=bm=cm thì tam giác abc vuông tại a
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy M , trên tia đối của CB lấy N sao cho BM = CN
a) CM : tam giác AMN cân
b. kẻ BE vuông góc AM (E thuộc AM),CF vuông góc AN . CM:tam giác BME= tam giác CNF
c.EB cắt FC tại O. CM: AO là phân giác của góc MAN
d.qua M kẻ vuông góc AM,qua N kẻ vuông góc AN 2 đường thẳng cắt nhau tại H . CM: A , O , H thẳng hàng
a: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góckề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
b: Xét ΔBME vuông tại E và ΔCNF vuông tại F có
BM=CN
\(\widehat{BME}=\widehat{CNF}\)(ΔABM=ΔACN)
Do đó: ΔBME=ΔCNF
c: Ta có: ΔBME=ΔCNF
=>ME=NF
Ta có: AE+EM=AM
AF+FN=AN
mà AM=AN và ME=NF
nên AE=AF
Xét ΔAEO vuông tại E và ΔAFO vuông tại F có
AO chung
AE=AF
Do đó: ΔAEO=ΔAFO
=>\(\widehat{EAO}=\widehat{FAO}\)
=>\(\widehat{MAO}=\widehat{NAO}\)
=>AO là phân giác của góc MAN
d: Xét ΔAMH vuông tại M và ΔANH vuông tại N có
AH chung
AM=AN
Do đó: ΔAMH=ΔANH
=>\(\widehat{MAH}=\widehat{NAH}\)
=>AH là phân giác của góc MAN
mà AO là phân giác của góc MAN
nên A,O,H thẳng hàng
Đúng 1
Bình luận (0)
a,cho tam giác ABC góc B =90độ biết AC=10cm ,AB=8cm.tính BC
b,cho tam giác ABC cân tại A trên tia đối của BC lấy H.trên tia đối của CB lấy K sao cho BH=CK
1,cm tam giác AKH cân
2,kẻ BM vuông AH taih M .kẻ CN vuông AK tại N .cm BM=CN
3,cm AM =AN
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy M , trên tia đối của CB lấy N sao cho BM = CN
a) CM : tam giác ABM= tam giác ACN
b) Kẻ BH vuông góc với AM tại H, CK vuông góc với AN tại K
CM: BH=CK
c) CM: HK//BC
d ) Gọi O là giao điểm của HB và KC. Chứng minh tam giác OBC cân.
Làm nhanh giúp mình nhaa. Cám ơn nhìuu<33
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó:ΔABM=ΔACN
b: Xét ΔHMB vuông tại H và ΔKNC vuông tại K có
MB=NC
\(\widehat{M}=\widehat{N}\)
Do đó: ΔHMB=ΔKNC
Suy ra: BH=CK
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
BH=CK
Do đó:ΔABH=ΔACK
Suy ra: AH=AK
Xét ΔAMN có AH/AM=AK/AN
nên HK//MN
hay HK//BC
d: Ta có: ΔHBM=ΔKCN
nên \(\widehat{HBM}=\widehat{KCN}\)
=>\(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
Đúng 1
Bình luận (1)
cho hình tam giác abc trên BC lấy M sao cho BM = 1/4 BC Nối A với M trên ab lấy N sao cho n m = 1/3 am nối b với n biết diện tích tam giác b m n bằng 8 cm vuông Tính diện tích tam giác ABC
Trên AB lấy N xong lại nối B với N???
Check lại đề đi em
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, B30độ. Trên cạnh BC lấy M sao cho AMBM. Chứng minh tam giác AMC đều.c ABCvuông tại A, 30B. Trên cạnh B
Đọc tiếp
Cho tam giác ABC vuông tại A, B=30độ. Trên cạnh BC lấy M sao cho AM=BM. Chứng minh tam giác AMC đều.c
ABCvuông tại A, 30B=. Trên cạnh B
Xét ΔABM có : BA=BM
=> ΔABM cân tại B
=> \(\widehat{BAM}=\widehat{B}=30^o\)
=> \(\widehat{MAC}=90^o-30^o=60^o\)
\(\widehat{C}=90^o-\widehat{B}=60^o\)
ΔAMC có 2 góc \(60^o\)
=> ΔAMC là tam giác đều
Đúng 0
Bình luận (1)
Cho tam giác ABC cân tại A có ^A=45 độ. Từ trung điểm I cảu AC vẽ đường thẳng vuông góc với AC nó cắt BC ở M. Trên tia đối tia AM lấy N sao cho AN=BM
a, tính ^B và ^ C của tam giác ABC
b, CM: ^AMC=^ABC
c, CM: tam giác ABM = tam giác CAN
d, CM: tam giác MNC vuông cân
cho tam giác abc cân tại a trên tia đối của bc lấy điểm m trên tia đối của tia cb lấy điểm n sao cho bm=cn kẻ bh vuông góc với am và kẻ ck vuông góc với an
a. CM tam giác ahb=tam giác ahc
b. Cm hk sông sông với bc
tui đang cần câu b thôi nha , giải nhanh giúp tui vs nha
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
b: Xét ΔAMN có
AH/AM=AK/AN
nên HK//MN
hay KH//BC
Đúng 0
Bình luận (0)
cho tam giác abc cân tại a . kẻ ah vuông góc với bc tại h trên tia đối của cb lấy diểm n trên tia đối của bc lấy điểm m sao cho bm= cn . cm tam giác amn cân
kẻ bd vuông góc với am tại d , ce vuông góc với an tại e , ce cắt bd tại k . chứng minh 3 điểm a,h,k thẳng hàng
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
=>ΔABM=ΔACN
=>AM=AN
b: góc MBD=góc ECN
=>góc KBC=góc KCB
=>K nằm trên trung trực của BC
=>A,H,K thẳng hàng
Đúng 0
Bình luận (0)















