Xét ΔABM có : BA=BM
=> ΔABM cân tại B
=> \(\widehat{BAM}=\widehat{B}=30^o\)
=> \(\widehat{MAC}=90^o-30^o=60^o\)
\(\widehat{C}=90^o-\widehat{B}=60^o\)
ΔAMC có 2 góc \(60^o\)
=> ΔAMC là tam giác đều
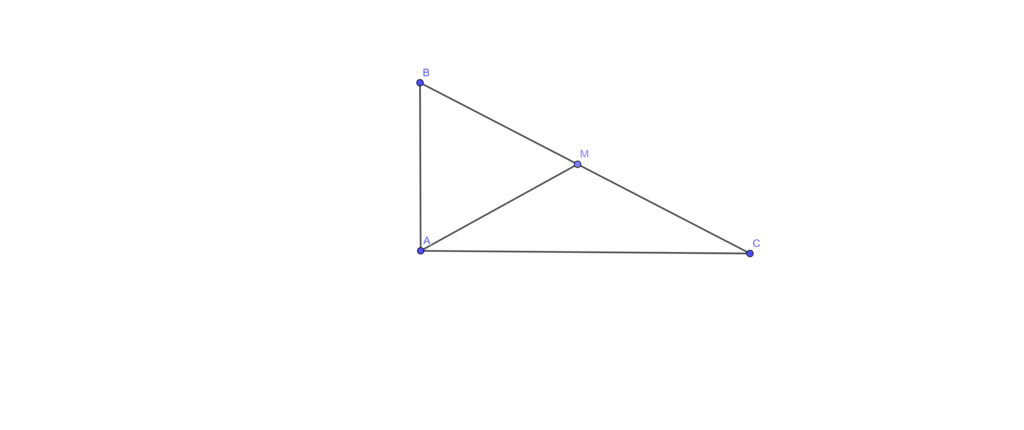
Bài 4. Cho tam giác ABC vuông tại A có C = 30 deg Trên cạnh BC lấy điểm M sao cho BM = BA. Chứng minh rằng: a) tâm giác AMB đều. b) AM = (BC)/2 c) Kẻ phân giác của góc AMC cắt Ac tại D. CM:AB//MD.
Cho tam giác ABC cân tại A, cạnh đáy < cạnh bên. Trên tia đối của tia BC lấy điểm M sao cho MA = MC. Trên tia đối của AM lấy điểm N sao cho AN = BM. a) Chứng minh góc AMC = BAC; b) Chứng minh CM = CN; c) Tìm điều kiện của TG ABC để CM vuông góc với CN.
Cho tam giác ABC vuông tại A . Trên cạnh BC lấy điểm M sao cho BM = BA . Chứng minh
a) tam giác AMB là tam giác đều
b) AM = BC/2
Cho tam giác ABC vuông tại A . Trên cạnh BC lấy điểm M sao cho BM = BA . Chứng minh
a) tam giác AMB đều
b) AM= BC/2
Cho tam giác ABC vuông tại A, góc =30 độ. Trên cạnh BC lấy M sao cho AM=BM. Chứng minh: AC=BC:2
Bài 1. Cho tam giác ABC vuông tại A có góc B= 53 độ
a) Tính góc C.
b) Trên cạnh BC, lấy một điểm D sao cho BD=BA. Tia phân giác của góc B cắt cạnh AC ở điểm E. Chứng minh tam giác BEA = tam giác BED.
Bài 2. Cho tam giác ABC có AB= AC và M là trung điểm của cạnh BC.
a) Chứng minh tam giác AMB = tam giác AMC.
b) Qua A, vẽ đường thẳng a vuông góc với AM. Chứng minh AM vuông góc với BC và a song song với BC.
c) Qua C, vẽ đường thẳng b song song với AM. Gọi N là giao điểm của hai đường thẳng a và b. Chứng minh tam giác AMC = tam giác CNA.
Bài 3. Cho tam giác ABC, gọi M là trung điểm của cạnh BC. Trên tia đối của tia MAlấy điểm D sao cho MD = MA.
a) Chứng minh tam giác MAB = tam giác MDC.
b) Chứng minh rằng AB = CD và AB // CD.
Bài 4. Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA. Vẽ AH vuông góc với BC tại H.
a) Chứng minh rằng: tam giác ABD = tam giác EBD và AD = ED.
b) Chứng minh rằng: AH // DE.
*Vẽ hình giúp mình*
Cho tam giác ABC cân tại A, có cạnh đáy nhỏ hơn cạnh bên. Đường trung trực cuae AC cắt đường thẳng BC tại M. Trên tia đối tia AM lấy điểm N sao cho AN = BM
a, Chứng minh góc AMC = góc BAC
b, chứng minh CM = CN
Cho tam giác ABC cân tại A . Vẽ AM vuông góc với BC ( M thuộc BC )
a) Chứng minh tam giác ABM = tam giác ACM
b) trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm E sao cho AD = AE . Chứng minh tam giác ABE = tam giác ACD và DE song song với BC
c) Gọi I là giao điểm của BE và CD . Chứng minh AI là tia phân giác của góc BAC
Cho tam giác ABC vuông tại A (AB>AC) Có BE là đường phân giác của góc ABC ( E thuộc AC) trên cạnh BC lấy điểm H sao cho BA=BH
a) chứng minh tam giác ABE= tam giác HBE
b) Chứng minh EH vuông góc với BC
c) Trên tia BA lấy điểm M sao cho BM=BC chứng minh EM=EC
d) Chứng minh BC-BA>EC-EA
