Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).

Theo định lí tổng ba góc của tam giác ta có:

    a + b + c = 180.

Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:

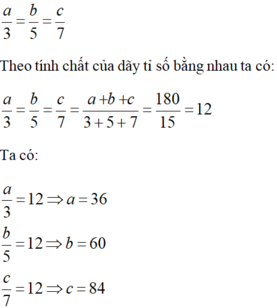
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

Tổng số đo các góc của hình tam giác luôn bằng 360 độ

Số đo của góc A là:360:(3+5+7)x3=72 độ

Số đo của góc B là:72:3x5=120 độ

Số đo của góc C là:360-120-72=168 độ

Góc A = 72^o

Góc B = 120^o

Góc C = 168^o

A=36

B=60

C=84

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

gọi số đo 3 góc là a,b,c(a,b,c>0)

Áp dụng t/c dtsbn ta có:

\(\dfrac{a}{15}=\dfrac{b}{6}=\dfrac{c}{9}=\dfrac{a+b+c}{15+6+9}=\dfrac{180^o}{30}=6^o\)

\(\dfrac{a}{15}=6^o\Rightarrow a=90^o\\ \dfrac{b}{6}=6^o\Rightarrow b=36^o\\ \dfrac{c}{9}=6^o\Rightarrow c=54^o\)

Gọi 3 góc của tam giác là a,b,c(độ;a>b>c>0)

Áp dụng tc dtsbn:

\(\dfrac{a}{15}=\dfrac{b}{9}=\dfrac{c}{6}=\dfrac{a+b+c}{15+6+9}=\dfrac{180}{30}=6\\ \Leftrightarrow\left\{{}\begin{matrix}a=90\\b=54\\c=36\end{matrix}\right.\)

Vậy ...

Gọi số đo từng góc của tam giác là: x,y,z(bạn đặt đk nhé)
ta có:  \(\dfrac{x+y+z}{15+6+9}=\dfrac{180}{30}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=6.15=90\\y=6.6=36\\z=6.9=54\end{matrix}\right.\)

Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta được:

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)

\(\Rightarrow\widehat{A}=12^o.3=36^o\)

\(\widehat{B}=12^o.5=60^o\)

\(\widehat{C}=12^o.7=84^o\)

nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)

vậy : A = 3 . 12 = 36

B = 5 . 12 = 60

C = 7 . 12 = 84

=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)

Gọi số đo của các góc A,B,C trong tam giác ABC lần lượt là là a,b,c

Ta có: \(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}\) và tổng ba góc là 180^o

Áp dụng tính chất của dãy tỉ số bằng nhau

\(\dfrac{a}{3}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c}{3+5+7}=\dfrac{180^o}{15}=12^o\)

+) Nếu \(\dfrac{a}{3}=12\)⇒ a= 36^o

+)Nếu \(\dfrac{b}{5}\)=12⇒b=60^o

+)Nếu \(\dfrac{c}{7}\)=12⇒c=84^o

Vậy góc A bằng 36^o, góc B bằng 60^o, góc C bằng 84^o

Câu 1: C

Câu 2: D

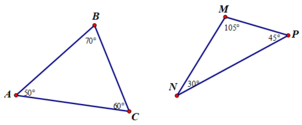
ΔABC có tổng ba góc là : 50o + 60o + 70o = 180o

ΔMNP có tổng ba góc là : 30o + 45o + 105o = 180o

Nhận xét: Tổng ba góc của hai tam giác đều là 1800