ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{3}\)

\(tan3x=tanx\)

\(\Leftrightarrow3x=x+k\pi\)

\(\Leftrightarrow x=\dfrac{k\pi}{2}\)

Đối chiếu điều kiện ta được \(x=k\pi\) là nghiệm của phương trình.

Giải theo công thức tan(x+2x)=(tanx+tan2x)/(1-tanx.tan2x) có vẻ nhanh hơn đó. 

Nhưng nhớ phải đặt điều kiện cho 3 cái cos dưới mẫu khác 0 (đk riêng của pt lượng giác)

Giải phương trình : sin5x-sin3x=0

Đáp án A

Tìm điều kiện để phương trình ban đầu có nghĩa. Giải trực tiếp phương trình đã cho và đối chiếu điều kiện để suy ra nghiệm cần tìm.

Điều kiện

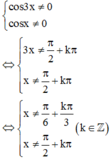
Ta có 

Đối chiếu với điều kiện

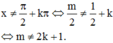
Khi đó 

Từ 

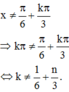
Do vế phải của biểu thức trên không là số nguyên nó luôn đúng.

Vậy nghiệm của phương trình 

Đáp án C.

Điều kiện cos 3 x ≢ 0 cos x ≢ 0 ⇔ 3 x ≢ π 2 + k π x ≢ π 2 + k π ⇔ x ≢ π 6 + k π 3 x ≢ π 2 + k π  

⇔ x ≢ π 6 + k π 3 , k ∈ ℤ  .

Phương trình tan 3 x = tan x ⇔ sin 3 x cos 3 x = sin x cos x ⇔ sin 3 x . cos x - cos 3 x . sin x = 0  

⇔ sin 2 x = 0 ⇔ 2 x = k π ⇔ x = k π 2 , k ∈ ℤ . Do x ≢ π 6 + k π 3 nên x = k π , k ∈ ℤ  .

Nếu x ∈ 0 ; 2018 π thì  0 < k π < 2018 π ⇔ 0 < k < 2018

→ k ∈ ℤ k ∈ 1 ; 2 ; . . . . ; 2017 . . Vậy có 2017 - 1 + 1 = 2017  giá trị k nguyên thỏa mãn nên phương trình có 2017 nghiệm.

`tan3x=tanx`

`<=>3x=x+kπ`

`<=>x=k π/2`

Phương trình có `4` điểm biểu diễn các nghiệm: `π/2 ; π ; (3π)/2 ; 2π`.

Để giải các phương trình này, chúng ta cần sử dụng các quy tắc và công thức của hàm tan và hàm cot. Hãy xem cách giải từng phương trình một:

a) Để giải phương trình tan(x) = -1, ta biết rằng giá trị của hàm tan là -1 tại các góc -π/4 và 3π/4. Vì vậy, x có thể là -π/4 + kπ hoặc 3π/4 + kπ, với k là số nguyên.

b) Để giải phương trình tan(x+20°) = tan(60°), ta có thể sử dụng quy tắc tan(A+B) = (tanA + tanB) / (1 - tanAtanB). Áp dụng công thức này, ta có: (tanx + tan20°) / (1 - tanxtan20°) = tan60°. Giải phương trình này, ta sẽ tìm được giá trị của x.

c) Để giải phương trình tan(3x) = tan(x-π/6), ta có thể sử dụng quy tắc tan(A-B) = (tanA - tanB) / (1 + tanAtanB). Áp dụng công thức này, ta có: (tan3x - tan(π/6)) / (1 + tan3xtan(π/6)) = 0. Giải phương trình này, ta sẽ tìm được giá trị của x.

d) Để giải phương trình tan(5x+π/4) = 0, ta biết rằng giá trị của hàm tan là 0 tại các góc π/2 + kπ, với k là số nguyên. Vì vậy, 5x+π/4 = π/2 + kπ. Giải phương trình này, ta sẽ tìm được giá trị của x.

e) Để giải phương trình cot(2x-π/4) = 0, ta biết rằng giá trị của hàm cot là 0 tại các góc π + kπ, với k là số nguyên. Vì vậy, 2x-π/4 = π + kπ. Giải phương trình này, ta sẽ tìm được giá trị của x.

a: tan x=-1

=>tan x=tan(-pi/4)

=>x=-pi/4+kpi

b: tan(x+20 độ)=tan 60 độ

=>x+20 độ=60 độ+k*180 độ

=>x=40 độ+k*180 độ

c: tan 3x=tan(x-pi/6)

=>3x=x-pi/6+kpi

=>2x=-pi/6+kpi

=>x=-pi/12+kpi/2

d: tan(5x+pi/4)=0

=>5x+pi/4=kpi

=>5x=-pi/4+kpi

=>x=-pi/20+kpi/5

e: cot(2x-pi/4)=0

=>2x-pi/4=pi/2+kpi

=>2x=3/4pi+kpi

=>x=3/8pi+kpi/2