tam giác ABC cân tại A Gọi M N D theo thứ tự là trung điểm AB AC BC
chứng minh AMDN là hình thoi
Những câu hỏi liên quan
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Chứng minh rằng ADEF là hình thoi
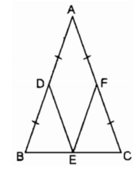
Ta có: E là trung điểm của BC (gt)
D là trung điểm của AB (gt) nên ED là đường trung bình của ∆ ABC
DE = AF = 1/2 AC (1)
F là trung điểm của AC (gt) nên EF là đường trung bình ∆ ABC ⇒ EF = AD = 1/2 AB (2)
AB = AC (gt)
Từ (1), (2) và (gt) suy ra: AD = DE = EF = AF
Vậy tứ giác ADEF là hình thoi.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Qua điểm D ϵ cạnh BC, kẻ đường thẳng vuông góc với BC, cắt cạnh AB, AC theo thứ tự ở E và F. Gọi M, N là thứ tự theo trung điểm của BE và CF. CMR:
a) Tứ giác AMDN là hình chữ nhật?
b) AD=MN?
ủa, bạn tên đầy đủ là gì?
Cho tam giác ABC cân tại A. Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC
a) Chứng minh rằng ADEFF là hình thoi
b) Tam giác ABC có thêm điều kiện gì thì ADEF là hình vuông
a) Tứ giác ADEF có bốn cạnh bằng nhau nên là hình thoi.
b) Hình thoi ADEF là hình vuông \(\Leftrightarrow\widehat{A}=90^o\Leftrightarrow\Delta ABC\) vuông cân tại A.
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A. Gọi D;E;F theo thứ tự là trung điểm các cạnh AB,BC,CA.Chứng minh rằng tứ giác ADEF là hình thoi.
Cho tam giác ABC vuông tại A, trung tuyến AD .Gọi M,N theo thứ tự là điểm đối xứng của B,D qua AC . Chứng minh :
a)Tứ giác ANCD là hình thoi
b)Tứ giác ABDN là hình bình hành
c)Tứ giác BDMN là hình thang cân
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB, AC, BC. a)Tứ giác MNBC và tứ giác MNBH là hình gì? vì sao?b)Gọi D là điểm đối xứng với H qua N. Chứng minh ADCH là hình chữ nhật c)Kẻ DE vuông góc với AC, gọi K là trung điểm của EC. Qua K vẽ đường thẳng d vuông góc với DK. Chứng minh: Ba đường thẳng AH, MN và d đồng qui ( cùng gặp nhau tại một điểm )Giúp em với các cao nhân ơiii
Đọc tiếp
Cho tam giác ABC cân tại A. Gọi M,N,H theo thứ tự là trung điểm của AB, AC, BC.
a)Tứ giác MNBC và tứ giác MNBH là hình gì? vì sao?
b)Gọi D là điểm đối xứng với H qua N. Chứng minh ADCH là hình chữ nhật
c)Kẻ DE vuông góc với AC, gọi K là trung điểm của EC. Qua K vẽ đường thẳng d vuông góc với DK. Chứng minh: Ba đường thẳng AH, MN và d đồng qui ( cùng gặp nhau tại một điểm )
Giúp em với các cao nhân ơiii
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: NM là đường trung bình của ΔABC
Suy ra: NM//BC và \(NM=\dfrac{BC}{2}\)
mà \(BH=CH=\dfrac{BC}{2}\)
nên NM=BH=CH
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{MBC}=\widehat{NCB}\)
nên BMNC là hình thang cân
Xét tứ giác MNHB có
MN//BH
MN=BH
Do đó: MNHB là hình bình hành
b: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH\(\perp\)BC
Xét tứ giác AHCD có
N là trung điểm của đường chéo AC
N là trung điểm của đường chéo HD
Do đó: AHCD là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCD là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn( ABAC) có M, N theo thứ tự là trung điểm của AB, BC.a) Biết AC 9cm. Tính MNb) Gọi E là điểm đối xứng của N qua M và P là trung điểm của CE. Đoạn CE cắt AB tại L. Chứng minh AEBN là hình bình hành và PC 3PLc) Vẽ đường cao AD của tam giác ABC. Gọi Q là điểm đối xứng của P qua BC. Chứng minh DPNQ là hình thoid) Tia QN cắt tia EA tại S. Chứng minh BNSE là hình thang cân
Đọc tiếp
Cho tam giác ABC nhọn( AB<AC) có M, N theo thứ tự là trung điểm của AB, BC.
a) Biết AC = 9cm. Tính MN
b) Gọi E là điểm đối xứng của N qua M và P là trung điểm của CE. Đoạn CE cắt AB tại L. Chứng minh AEBN là hình bình hành và PC = 3PL
c) Vẽ đường cao AD của tam giác ABC. Gọi Q là điểm đối xứng của P qua BC. Chứng minh DPNQ là hình thoi
d) Tia QN cắt tia EA tại S. Chứng minh BNSE là hình thang cân
Cho tam giác ABC vuông tại A, trung tuyến AD. Gọi M, N theo thứ tự là điểm đối xứng của B, D qua AC.
a) Chứng minh tứ giác ANCD là hình thoi.
b) Chứng minh tứ giác ABDN là hình bình hành.
c) Chứng minh tứ giác BDNM là hình thang cân.
d) Chứng minh DM đi qua trung điểm I cuả AN
Bài 1 : Cho tam giác cân ABC tại A. Gọi M , N , P theo thứ tự là trung điểm của AB , AC , BC . Cho Q là điểm đối xứng của P qua N. Chứng minh : a . MN // BC b . Tứ giác ANPB là hình thang . d . BMNC là hình thang cân . f . APCQ là hình chữ nhật c . PMAQ là hình thang . e . ABPQ là hình bình hành
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Đúng 0
Bình luận (0)